题目内容
【题目】已知圆![]() 与定点
与定点![]() ,动圆
,动圆![]() 过
过![]() 点且与圆
点且与圆![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若过定点![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于不同的两点
于不同的两点![]() 、
、![]() ,求弦长
,求弦长![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题设可知,动圆![]() 与定圆
与定圆![]() 相内切,结合椭圆的定义,即可求得动圆圆心
相内切,结合椭圆的定义,即可求得动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)弦长问题采用代入法,直线斜率不存在弦长为![]() ,直线斜率存在时,设
,直线斜率存在时,设![]() 坐标,直线
坐标,直线![]() 方程,联立椭圆与直线方程,通过
方程,联立椭圆与直线方程,通过![]() 和韦达定理表示出
和韦达定理表示出![]() ,最后运用换元法和函数的性质,确定最大值.
,最后运用换元法和函数的性质,确定最大值.
解:(1)设圆![]() 的半径为
的半径为![]() ,题意可知,点
,题意可知,点![]() 满足:
满足:
![]() ,
,![]() ,
,
所以,![]() ,
,
由椭圆定义知点![]() 的轨迹为以
的轨迹为以![]() 为焦点的椭圆,且
为焦点的椭圆,且![]()
进而![]() ,故轨迹
,故轨迹![]() 方程为:
方程为:![]() .
.
(2)当直线![]() 斜率不存在时,
斜率不存在时,![]() ,
,![]() 或
或![]() ,/span>
,/span>![]() ,
,
此时弦长![]() .
.
当直线![]() 斜率存在时,设
斜率存在时,设![]() 的方程为:
的方程为:![]() ,
,
由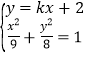 消去
消去![]() 得:
得:![]() ,
,
由△![]() 恒成立,
恒成立,
设![]() 、
、![]() ,可得:
,可得:
![]() ,
,![]() ,
,
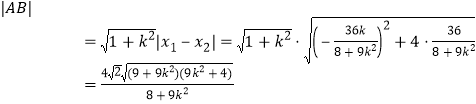 ,
,
令8![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
综上,弦长![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
【题目】某服装公司,为确定明年![]() 类服装的广告费用,对往年广告费
类服装的广告费用,对往年广告费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:件)和年利润
(单位:件)和年利润![]() (单位:千元)的影响.对2011-2018广告费
(单位:千元)的影响.对2011-2018广告费![]() 和年销售量
和年销售量![]() 数据进行了处理,分析出以下散点图和统计量:
数据进行了处理,分析出以下散点图和统计量:

|
|
|
|
|
|
|
45 | 580 | 2025 | 297 | 1600 | 960 | 1440 |
表中![]()
(1)由散点图可知,![]() 和
和![]() 更适合作为年销售量
更适合作为年销售量![]() 关于年广告费
关于年广告费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果和表中数据求![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)已知该类服装年利率![]() 与
与![]() 的关系为
的关系为![]() .由(2)回答以下问题:年广告费用
.由(2)回答以下问题:年广告费用![]() 等于60时,年销售量及年利润的预报值为多少?年广告费用为何值时,年利率的预报值最小?
等于60时,年销售量及年利润的预报值为多少?年广告费用为何值时,年利率的预报值最小?
对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: