题目内容
【题目】已知过抛物线y2＝4x的焦点F的弦长为36，求弦所在的直线方程．
【答案】y＝
(x－1)或y＝－(x－1).
【解析】
分析知直线的斜率存在且不为0，设直线方程并与抛物线方程联立，利用过焦点的弦长公式进行计算即可得到答案.
因为过焦点的弦长为36，
所以弦所在的直线的斜率存在且不为零．
故可设弦所在直线的斜率为k，
且与抛物线交于A(x1，y1)、B(x2，y2)两点．
因为抛物线y2＝4x的焦点为F(1，0)．
所以 直线的方程为y＝k(x－1)．
由
整理得k2x2－(2k2＋4)x＋k2＝0(k≠0)．
所以 x1＋x2＝
.
所以 |AB|＝|AF|＋|BF|＝x1＋x2＋2＝＋2.
又|AB|＝36，所以＋2＝36，所以 k＝±.
所以 所求直线方程为y＝ (x－1)或y＝－ (x－1)．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】某班主任为了对本班学生的月考成绩进行分析，从全班40名同学中随机抽取一个容量为6的样本进行分析．随机抽取6位同学的数学、物理分数对应如表：
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学分数x | 60 | 70 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 80 | 88 | 90 | 85 | 95 |
（1）根据上表数据用散点图说明物理成绩y与数学成绩x之间是否具有线性相关性？
（2）如果具有线性相关性，求出线性回归方程(系数精确到0.1)；如果不具有线性相关性，请说明理由．
（3）如果班里的某位同学数学成绩为50，请预测这位同学的物理成绩。
（附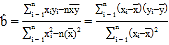
)
