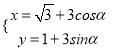题目内容
【题目】如图，在四棱锥P-ABCD中，底面ABCD是正方形，
平面ABCD，且
，点E为线段PD的中点.
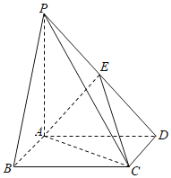
（1）求证：
平面AEC；
（2）求证：
平面PCD；
（3）求三棱锥
的体积.
【答案】（1）证明见解析；（2）证明见解析；（3）
【解析】
（1）连结BD，交AC于点O，连结OE．可得PB∥OE，再由线面平行的判定可得PB∥平面AEC；
（2）由PA=AD，E为线段PD的中点，得AE⊥PD，再由PA⊥平面ABCD，得PA⊥CD，由线面垂直的判定可得AE⊥平面PCD；
（3）根据AE⊥平面PCD，结合三棱锥的体积公式求出其体积即可．
(1)证明：连结BD，交AC于点O，连结OE，
如图示：
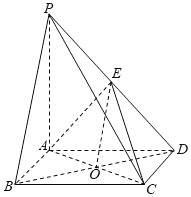
∵O是正方形ABCD对角线交点，∴O为BD的中点，
由已知E为线段PD的中点,∵PB∥OE，
又OE平面AEC，PB平面AEC，
∴PB∥平面AEC；
(2)证明：∵PA=AD，E为线段PD的中点，∴AE⊥PD，
∵PA⊥平面ABCD，∴PA⊥CD，
在正方形ABCD中，CD⊥AD，又PA∩AD=A，
∴CD⊥平面PAD，又AE平面PAD，
∴CD⊥AE，又PD∩CD=D，
∴AE⊥平面PCD；
(3)由
平面ABCD，
，点E为线段PD的中点，
∴
为等腰直角三角形，
，
底面ABCD是正方形，CD=3，
∵AE⊥平面PCD，
故三棱锥APCE的体积：
.
练习册系列答案
阅读快车系列答案
相关题目
