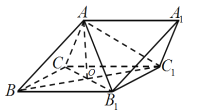
题目内容
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,D是BC的中点
,D是BC的中点
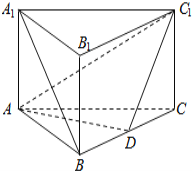 .
.
(1)求证:![]() 平面
平面![]() ;
;
![]() 2).求二面角
2).求二面角![]() 的大小.
的大小.
【答案】(1)见证明;(2)![]()
【解析】
(1)证明线面平行,可以利用线面平行的判定定理,只要证明 A1B∥OD即可;(2)可判断BA,BC,BB1两两垂直,建立空间直角坐标系,用坐标表示点与向量,求得平面ADC1的法向量、平面ADC的法向量,利用向量数量积可求二面角C1﹣AD﹣C的余弦值;
![]() 证明:连接
证明:连接![]() ,交
,交![]() 于点O,连接OD.
于点O,连接OD.
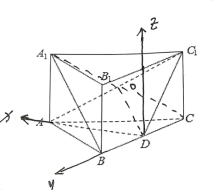
由![]() 是直三棱柱,
是直三棱柱,
得四边形![]() 为矩形,
为矩形,
O为![]() 的中点,又D为BC中点,
的中点,又D为BC中点,
所以OD为![]() 中位线,
中位线,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(2)过D点作![]() 的平行线,因为
的平行线,因为![]() 为直三棱柱,所以平行线
为直三棱柱,所以平行线
垂直于底面ABC
又因为![]() 且
且![]() ,所以三角形
,所以三角形![]() 为正三角形
为正三角形
所以![]() ,所以以D为坐标原点建立如图所示的空间直角坐标系
,所以以D为坐标原点建立如图所示的空间直角坐标系![]()
设![]() ,则
,则![]() ,所以D(0,0,0),
,所以D(0,0,0),![]() ,
,![]() ,
,![]()
所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
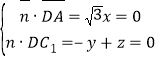 ,令
,令![]() ,得到
,得到![]()
又易知平面ADC与z轴垂直,
所以平面ADC的一个法向量![]()
所以![]() ,
,
由图可以看出二面角![]() 为锐角
为锐角
所以二面角![]() 的大小为
的大小为![]() 。
。

【题目】某种产品的质量以其“无故障使用时间![]() (单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
(单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
无故障使用时间 |
|
|
|
频数 | 20 | 40 | 40 |
以试验结果中无故障使用时间落入各组的频率作为一件产品的无故障使用时间落入相应组的概率.
(1)从该企业任取两件这种产品,求至少有一件是优质品的概率;
(2)若该企业生产的这种产品每件销售利润![]() (单位:元)与其无故障使用时间
(单位:元)与其无故障使用时间![]() 的关系式为
的关系式为
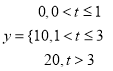
从该企业任取两件这种产品,其利润记为![]() (单位:元),求
(单位:元),求![]() 的分布列与数学期望.
的分布列与数学期望.
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为![]() =0.06e0.2303x,且相关指数R2=0.9522.
=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为

![]() =
=![]()
![]() ;相关指数R2=
;相关指数R2= .
.