题目内容
【题目】如图,已知正三棱锥P﹣ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.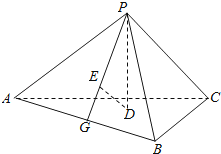
(1)证明:G是AB的中点;
(2)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
【答案】
(1)
证明:∵P﹣ABC为正三棱锥,且D为顶点P在平面ABC内的正投影,
∴PD⊥平面ABC,则PD⊥AB,
又E为D在平面PAB内的正投影,
∴DE⊥面PAB,则DE⊥AB,
∵PD∩DE=D,
∴AB⊥平面PDE,连接PE并延长交AB于点G,
则AB⊥PG,
又PA=PB,
∴G是AB的中点;
(2)
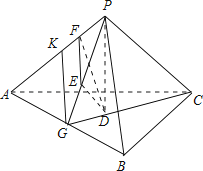 ∵正三棱锥P﹣ABC的侧面是直角三角形,
∵正三棱锥P﹣ABC的侧面是直角三角形,
∴PB⊥PA,PB⊥PC,则PB⊥平面PAC,
而PB平面PAB,则平面PAB⊥平面PAC,
在平面PAB中,过E作EF⊥PA,则EF⊥平面PAC,
即F为E在平面PAC内的正投影.
由于PA=PB=PC=6,故AB=BC=AC=6 ![]() ,
,
易知PG= ![]() =3
=3 ![]() ,GD=
,GD= ![]() =
= ![]() ,由勾股定理得PD=
,由勾股定理得PD= ![]() =2
=2 ![]() ,
,
【解析】(Ⅰ)根据题意分析可得PD⊥平面ABC,进而可得PD⊥AB,同理可得DE⊥AB,结合两者分析可得AB⊥平面PDE,进而分析可得AB⊥PG,又由PA=PB,由等腰三角形的性质可得证明;(2)由线面垂直的判定方法可得PB⊥平面PAC,进而由于PB平面PAB,可得平面PAB⊥平面PAC,由此可以在平面PAB中,过E作EF⊥PA,可得F为E在平面PAC内的正投影.
进而由棱锥的体积公式计算可得答案.;本题考查几何体的体积计算以及线面垂直的性质、应用,解题的关键是正确分析几何体的各种位置、距离关系.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

