题目内容
【题目】如图,设椭圆C: ![]() +y2=1(a>1)
+y2=1(a>1)
(1)求直线y=kx+1被椭圆截得到的弦长(用a,k表示)
(2)若任意以点A(0,1)为圆心的圆与椭圆至多有三个公共点,求椭圆的离心率的取值范围.
【答案】
(1)
由题意可得: 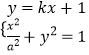 ,可得:(1+a2k2)x2+2ka2x=0,
,可得:(1+a2k2)x2+2ka2x=0,
得x1=0或x2= ![]() ,
,
直线y=kx+1被椭圆截得到的弦长为: ![]() =
= ![]()
(2)
假设圆A与椭圆由4个公共点,由对称性可设y轴左侧的椭圆上有两个不同的点P,Q,满足|AP|=|AQ|,
记直线AP,AQ的斜率分别为:k1,k2;且k1,k2>0,k1≠k2,由(1)可知|AP|= ![]() ,|AQ|=
,|AQ|= ![]() ,
,
故: ![]() =
= ![]() ,所以,(k12﹣k22)[1+k12+k22+a2(2﹣a2)k12k22]=0,由k1≠k2,
,所以,(k12﹣k22)[1+k12+k22+a2(2﹣a2)k12k22]=0,由k1≠k2,
k1,k2>0,可得:1+k12+k22+a2(2﹣a2)k12k22=0,
因此 ![]() a2(a2﹣2)①,
a2(a2﹣2)①,
因为①式关于k1,k2;的方程有解的充要条件是:1+a2(a2﹣2)>1,
所以a> ![]() .
.
因此,任意点A(0,1)为圆心的圆与椭圆至多有三个公共点的充要条件为:1<a<2,
e= ![]() =
= ![]() 得,所求离心率的取值范围是:
得,所求离心率的取值范围是: ![]()
【解析】(1)联立直线y=kx+1与椭圆方程,利用弦长公式求解即可.(2)写出圆的方程,假设圆A与椭圆由4个公共点,再利用对称性有解已知条件可得任意一A(0,1)为圆心的圆与椭圆至多有3个公共点,a的取值范围,进而可得椭圆的离心率的取值范围.本题考查直线与椭圆的位置关系的综合应用,椭圆与圆的位置关系的综合应用,考查分析问题解决问题的能力,考查转化思想以及计算能力.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目