题目内容
17.已知x>0,y>0,x+2y-xy=0.(Ⅰ)求xy的最小值;
(Ⅱ)求x+y的最小值.
分析 (I)由于x>0,y>0,x+2y-xy=0.变形利用基本不等式的性质即可得出.
(II)由x+2y=xy,解得y=$\frac{x}{x-2}$>0,解得x>2.变形x+y=x+$\frac{x}{x-2}$=x-2+$\frac{2}{x-2}$+3,再利用基本不等式的性质即可得出.
解答 解:(I)∵x>0,y>0,x+2y-xy=0.
∴xy=x+2y$≥2\sqrt{x•2y}$,化为xy≥8,当且仅当x=2y=4时取等号.
∴xy的最小值是8;
(II)由x+2y=xy,解得y=$\frac{x}{x-2}$>0,解得x>2.
∴x+y=x+$\frac{x}{x-2}$=x-2+$\frac{2}{x-2}$+3≥2$\sqrt{(x-2)•\frac{2}{x-2}}$+3=2$\sqrt{2}$+3,当且仅当x=2+$\sqrt{2}$,y=1+$\sqrt{2}$时取等号.
∴x+y的最小值为2$\sqrt{2}$+3.
点评 本题考查了基本不等式的性质,考查了变形能力、推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
7.如图所示,平面内z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,则|z1+z2|=( )
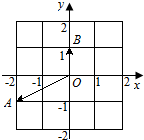

| A. | 2 | B. | 3 | C. | 2 $\sqrt{2}$ | D. | 3 $\sqrt{3}$ |
5.如果数列{an}中,满足a1,$\frac{{a}_{2}}{{a}_{1}}$,$\frac{{a}_{3}}{{a}_{2}}$,…,$\frac{{a}_{n}}{{a}_{n-1}}$是首项为1公比为3的等比数列,则a100等于( )
| A. | 3100 | B. | 390 | C. | 34950 | D. | 35050 |
12.在△ABC中,不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$≥$\frac{9}{π}$成立;在四边形ABCD中,不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$≥$\frac{16}{2π}$成立;在五边形ABCDE中,$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$+$\frac{1}{E}$≥$\frac{25}{3π}$成立.猜想在n边形中,成立的不等式为( )
| A. | $\frac{1}{{A}_{1}}$+$\frac{1}{{A}_{2}}$+…$\frac{1}{{A}_{n}}$≥$\frac{n}{π}$ | B. | $\frac{1}{{A}_{1}}$+$\frac{1}{{A}_{2}}$+…$\frac{1}{{A}_{n}}$≥$\frac{{n}^{2}}{(n+1)π}$ | ||
| C. | $\frac{1}{{A}_{1}}$+$\frac{1}{{A}_{2}}$+…$\frac{1}{{A}_{n}}$≥$\frac{{n}^{2}}{(n-2)π}$ | D. | $\frac{1}{{A}_{1}}$+$\frac{1}{{A}_{2}}$+…$\frac{1}{{A}_{n}}$≥$\frac{{n}^{2}}{(n+2)π}$ |
2.已知cos(π-α)=-$\frac{5}{13}$且α是第四象限角,则sinα=( )
| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | ±$\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
6.在△ABC中,已知A是三角形的内角,且sinA+cosA=$\frac{3}{5}$,则△ABC一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 无法确定三角形的形状 |
7.Sn是等差数列{an}的前n项和,若a2+a4+a15是一个确定的常数,则在数列{Sn}中也是确定常数的项是( )
| A. | S7 | B. | S4 | C. | S13 | D. | S16 |