题目内容
20.长为a的正六边形ABCDEF在平面α内,过A点作PA⊥α,PA=a,则P到CD的距离为2a,P到BC的距离为$\frac{\sqrt{7}}{2}$a.分析 先证明PC垂直于CD,然后在直角三角形PAC中利用勾股定理求出PC即可;同理先证明PQ垂直于BC,然后在直角三角形PAQ中利用勾股定理求出PQ即可求出所求.
解答  解:连接AC,CD⊥AC
解:连接AC,CD⊥AC
∵PA⊥平面a,CD?平面a
∴PA⊥CD,而PA∩AC=A
∴CD⊥平面PAC,则PC⊥CD
在直角三角形PAC中,AC=$\sqrt{3}$a,PA=a,
根据勾股定理可知PC=2a
即P到CD的距离为2a;
过点A作BC的垂线交BC的延长线于点Q,连接PQ
在直角三角形PAQ中,AQ=$\frac{\sqrt{3}}{2}$a,PA=a
根据勾股定理可知PQ=$\frac{\sqrt{7}}{2}$a.
∴P到BC的距离为$\frac{\sqrt{7}}{2}$a.
故答案为:2a,$\frac{\sqrt{7}}{2}$a.
点评 本题主要考查了空间点到直线的距离,以及线面垂直的判定和性质,同时考查了空间想象能力、计算能力,转化与划归的思想,属于中档题.

练习册系列答案
相关题目
10.已知$\overrightarrow a$=(3,0),$\overrightarrow b$=(-5,5)则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
15.已知a=0.2-0.2,b=log0.52,c=$\frac{\root{3}{2}}{2}$,则a,b,c的大小关系正确的是( )
| A. | a<b<c | B. | b<c<a | C. | c<b<a | D. | c<a<b |
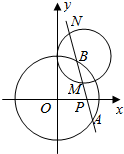 已知圆C过点P(0,5),Q(4,3),且圆心C在直线x-y+3=0上.
已知圆C过点P(0,5),Q(4,3),且圆心C在直线x-y+3=0上.