题目内容
9.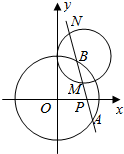 已知圆C过点P(0,5),Q(4,3),且圆心C在直线x-y+3=0上.
已知圆C过点P(0,5),Q(4,3),且圆心C在直线x-y+3=0上.(1)求圆C的方程;
(2)如图,过点P(4,0)做直线l与圆O:x2+y2=25交于点A,B,与圆C交于点M,N,若AB=MN,求直线l的方程.
分析 (1)设圆心C(a,a+3),根据圆C过点P(0,5),Q(4,3),可得CP2=CQ2,求得a的值,可得圆C的圆心和半径CP,从而求得圆C的方程.
(2)当直线l的斜率存在时,用点斜式设出直线l的方程,求得 圆心O到直线l的距离为d,可得弦长AB,同理求得MN,再根据AB=MN,求得k的值,从而求得直线l的方程.当直线l的斜率不存在时,检验满足条件,从而得出结论.
解答 解:(1)设圆心C(a,a+3),根据圆C过点P(0,5),Q(4,3),
可得CP=CQ,即CP2=CQ2,即a2+(a+3-5)2=(a-4)2+(a+3-3)2,
求得a=3,可得圆C的半径为CP=$\sqrt{{3}^{2}{+(6-5)}^{2}}$=$\sqrt{10}$,
故圆C的方程为 (x-3)2+(y-6)2=10.
(2)当直线l的斜率存在时,设直线l的方程为y-0=k(x-4),即kx-y-4k=0,
圆心O到直线l的距离为d=$\frac{|0-0-4k|}{\sqrt{{k}^{2}+1}}$=$\frac{|4k|}{\sqrt{{k}^{2}+1}}$,圆O的半径为5,故弦长AB=2$\sqrt{{R}^{2}{-d}^{2}}$=2$\sqrt{25-\frac{1{6k}^{2}}{{k}^{2}+1}}$.
圆心C(3,6)到直线l的距离为d=$\frac{|3k-6-4k|}{\sqrt{{k}^{2}+1}}$=$\frac{|k+6|}{\sqrt{{k}^{2}+1}}$,圆O的半径为$\sqrt{10}$,故弦长MN=2$\sqrt{{R}^{2}{-d}^{2}}$=2$\sqrt{10-\frac{{(k+6)}^{2}}{{k}^{2}+1}}$.
再根据AB=MN,可得2$\sqrt{25-\frac{{16k}^{2}}{{k}^{2}+1}}$=2$\sqrt{10-\frac{{(k+6)}^{2}}{{k}^{2}+1}}$,求得k=-$\frac{17}{4}$,故直线l的方程为-$\frac{17}{4}$x-y-17=0,即 17x+4y+68=0.
当直线l的斜率不存在时,直线l的方程为x=4,
圆心O到直线l的距离为d=4,圆O的半径为5,故弦长AB=2$\sqrt{{R}^{2}{-d}^{2}}$=6.
圆心C(3,6)到直线l的距离为d=1,圆O的半径为$\sqrt{10}$,故弦长MN=2$\sqrt{{R}^{2}{-d}^{2}}$=6,
满足AB=MN.
综上可得,直线l的方程为17x+4y+68=0或x=4.
点评 本题主要考查求圆的标准方程,直线和圆相交的性质,弦长公式的应用,体现了转化、分类讨论的数学思想,属于中档题.

| A. | f(2sin$\frac{5π}{7}$)<f(π)<f(4) | B. | f(4)<f(π)<f(2sin$\frac{5π}{7}$) | C. | f(π)<f(2sin$\frac{5π}{7}$)<f(4) | D. | f(4)<f(2sin$\frac{5π}{7}$)<f(π) |
| A. | y=x3 | B. | y=|x|+1 | C. | y=-x2+1 | D. | y=2-|x| |
| A. | M=N | B. | M?N | C. | M?N | D. | M∩N=∅ |
| A. | ¬p | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
 如图直角梯形OADC中,OA∥CD,∠D=60°,OA=1,CD=2,在梯形内挖去一个以OA为半径的四分之一圆,图中阴影部分绕OC所在直线旋转一周,求该旋转体的体积和表面积.
如图直角梯形OADC中,OA∥CD,∠D=60°,OA=1,CD=2,在梯形内挖去一个以OA为半径的四分之一圆,图中阴影部分绕OC所在直线旋转一周,求该旋转体的体积和表面积.