题目内容
3．已知函数f（x）=x2-2ax+4在区间（1，2）上有且只有一个零点，求a的取值范围．分析 若函数f（x）=x2-2ax+4只有一个零点，则△=0，经检验不符合条件；则函数f（x）=x2-2ax+4有两个零点，进而f（1）•f（2）＜0，解得答案．
解答 解：若函数f（x）=x2-2ax+4只有一个零点，
则△=4a2-16=0，解得：a=±2，
此时函数的零点为±2不在区间（1，2）上，
即函数f（x）=x2-2ax+4有两个零点，
则f（1）•f（2）＜0，即（5-2a）（8-4a）＜0，
解得：a∈（2，$\frac{5}{2}$）
点评 本题考查的知识点是二次函数的图象图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．两条平行直线l1：3x-2y-1=0，l2：3x-2y+1=0的距离是（ ）
| A． | $\frac{{2\sqrt{13}}}{13}$ | B． | $\frac{{\sqrt{13}}}{13}$ | C． | $\frac{1}{13}$ | D． | $\frac{2}{13}$ |
18．
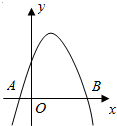如图所示为二次函数y=ax2+bx+c的图象，则|OA|•|OB|等于（ ）
如图所示为二次函数y=ax2+bx+c的图象，则|OA|•|OB|等于（ ）| A． | $\frac{c}{a}$ | B． | -$\frac{c}{a}$ | C． | ±$\frac{c}{a}$ | D． | -$\frac{a}{c}$ |
8．已知函数f（x）=x2+ax-c，g（x）=（$\frac{1}{2}$）x-m，若不等式f（x）＜0的解集为{x|-2＜x＜1}，若对任意的x1∈[-3，-2]，存在x2∈[0，2]，使f（x1）≥g（x2），则实数m的取值范围是（ ）
| A． | m≥$\frac{1}{4}$ | B． | m≥1 | C． | m≥0 | D． | m≥2 |
15．在复平面内，复数z=$\frac{2+i}{1-i}$，则其共轭复数z对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |