Question

【题目】已知椭圆C： + =1（a＞b＞0）的离心率为 ，过左焦点F且垂直于x轴的弦长为1．
（I）求椭圆C的标准方程；
（Ⅱ）点P（m，0）为椭圆C的长轴上的一个动点，过点P且斜率为 的直线l交椭圆C于A，B两点，问：|PA|2+|PB|2是否为定值？若是，求出这个定值并证明，否则，请说明理由．

Answer 1

【答案】解：（ I）由过左焦点F且垂直于x轴的弦长为1，

可知椭圆C过点 ，∴ ，

又∵e= = ，a2=b2+c2；

三式联立解得 ，

∴椭圆的方程为 +y2=1；

（ II）设P（m，0）（且﹣2≤m≤2），由已知，直线l的方程是y= （x﹣m），

由 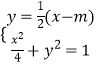，消去y得，2x2﹣2mx+m2﹣4=0，（*）

设A（x1，y1），B（x2，y2），则x1、x2是方程（*）的两个根，

所以有，x1+x2=m，x1x2= ，

所以，|PA|2+|PB|2=（x1﹣m）2+y12+（x2﹣m）2+y22

=（x1﹣m）2+ （x1﹣m）2+（x2﹣m）2+ （x2﹣m）2

= [（x1﹣m）2+（x2﹣m）2]

= [x12+x22﹣2m（x1+x2）+2m2]

= [（x1+x2）2﹣2m（x1+x2）﹣2x1x2+2m2]

= [m2﹣2m2﹣（m2﹣4）+2m2]=5（为定值）；

所以，|PA|2+|PB|2为定值

【解析】（Ⅰ）利用椭圆长轴长设出椭圆方程，利用点在椭圆上，求出b，即可得到椭圆方程．（Ⅱ）设出P，直线l的方程，联立直线与椭圆方程，设出A、B坐标，通过根与系数的关系，计算|PA|2+|PB|2，化简求解即可．