Question

【题目】设函数f（x）=|x|，g（x）=lg（ax2﹣4x+1），若对任意x1∈R，都存在在x2∈R，使f（x1）=g（x2），则实数a的取值范围是（　　）
A.（﹣∞，4]
B.（0，4]
C.（﹣4，0]
D.[0，+∞）

Answer 1

【答案】D
【解析】x1∈R，f（x）=|x|∈[0，+∞），
∵x2∈R，使f（x1）=g（x2），
∴g（x）=lg（ax2﹣4x+1）的值域包含[0，+∞），
当a=0时，g（x）=lg（﹣4x+1），显然成立；
当a≠0时，要使g（x）=lg（ax2﹣4x+1）的值域包含[0，+∞），
则ax2﹣4x+1的最小值小于等于1，
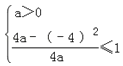∴ ， 即a＞0．
综上，a≥0．
∴实数a的取值范围是[0，+∞）．
故选：D．
【考点精析】通过灵活运用函数的值域，掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的即可以解答此题．