题目内容
【题目】已知函数![]() .
.
(1)若曲线![]() 的切线方程为
的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根据解析式求得导函数,设切点坐标为![]() ,结合导数的几何意义可得方程
,结合导数的几何意义可得方程![]() ,构造函数
,构造函数![]() ,并求得
,并求得![]() ,由导函数求得
,由导函数求得![]() 有最小值
有最小值![]() ,进而可知由唯一零点
,进而可知由唯一零点![]() ,即可代入求得
,即可代入求得![]() 的值;
的值;
(2)将![]() 解析式代入
解析式代入![]() ,结合零点定义化简并分离参数得
,结合零点定义化简并分离参数得![]() ,构造函数
,构造函数![]() ,根据题意可知直线
,根据题意可知直线![]() 与曲线
与曲线![]() 有两个交点;求得
有两个交点;求得![]() 并令
并令![]() 求得极值点,列出表格判断
求得极值点,列出表格判断![]() 的单调性与极值,即可确定与
的单调性与极值,即可确定与![]() 有两个交点时
有两个交点时![]() 的取值范围.
的取值范围.
(1)依题意,![]() ,
,![]() ,
,
设切点为![]() ,
,![]() ,
,
故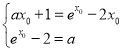 ,
,
故![]() ,则
,则![]() ;
;
令![]() ,
,![]() ,
,
故当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故当![]() 时,函数
时,函数![]() 有最小值,
有最小值,
由于![]() ,故
,故![]() 有唯一实数根0,
有唯一实数根0,
即![]() ,则
,则![]() ;
;
(2)由![]() ,得
,得![]() .
.
所以“![]() 在区间
在区间![]() 上有两个零点”等价于“直线
上有两个零点”等价于“直线![]() 与曲线
与曲线![]() 在
在![]() 有两个交点”;
有两个交点”;
由于![]() .
.
由![]() ,解得
,解得![]() ,
,![]() .
.
当![]() 变化时,
变化时,![]() 与
与![]() 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
| 3 |
|
|
| 0 | + | 0 |
|
|
| 极小值 |
| 极大值 |
|
所以![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又因为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
故当![]() 或
或![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 在
在![]() 上有两个交点,
上有两个交点,
即当![]() 或
或![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
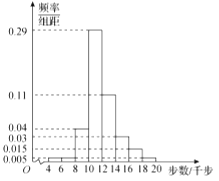
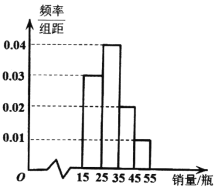
小学生10分钟应用题系列答案【题目】某企业对设备进行升级改造,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测一项质量指标值,该项质量指标值落在区间![]() 内的产品视为合格品,否则视为不合格品,如图是设备改造前样本的频率分布直方图,下表是设备改造后样本的频数分布表.
内的产品视为合格品,否则视为不合格品,如图是设备改造前样本的频率分布直方图,下表是设备改造后样本的频数分布表.
图:设备改造前样本的频率分布直方图
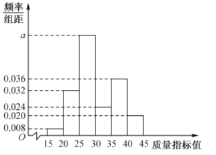
表:设备改造后样本的频率分布表
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)求图中实数![]() 的值;
的值;
(2)企业将不合格品全部销毁后,对合格品进行等级细分,质量指标值落在区间![]() 内的定为一等品,每件售价240元;质量指标值落在区间
内的定为一等品,每件售价240元;质量指标值落在区间![]() 或
或![]() 内的定为二等品,每件售价180元;其他的合格品定为三等品,每件售价120元,根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.若有一名顾客随机购买两件产品支付的费用为
内的定为二等品,每件售价180元;其他的合格品定为三等品,每件售价120元,根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.若有一名顾客随机购买两件产品支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好