题目内容
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)由椭圆的对称性知![]() 两点关于原点对称,不妨设
两点关于原点对称,不妨设![]() 在第一象限,由弦长可得
在第一象限,由弦长可得![]() ,代入
,代入![]() ,再结合
,再结合![]() 可解得
可解得![]() ;
;
(2)只要设出直线方程:![]() ,把
,把![]() 代入椭圆方程可解得M点坐标,同理可解得N点坐标,由两点求出直线MN的方程(注意分类讨论MN与
代入椭圆方程可解得M点坐标,同理可解得N点坐标,由两点求出直线MN的方程(注意分类讨论MN与![]() 垂直和不垂直两种情形),通过直线方程可观察出直线所过定点.
垂直和不垂直两种情形),通过直线方程可观察出直线所过定点.
详解:(1)根据题意,设直线![]() 与题意交于
与题意交于![]() 两点.不妨设
两点.不妨设![]() 点在第一象限,又
点在第一象限,又![]() 长为
长为![]() ,
,
∴![]() ,∴
,∴![]() ,可得
,可得![]() ,
,
又![]() ,
,
∴![]() ,故题意
,故题意![]() 的标准方程为
的标准方程为![]() ,
,
(2)显然直线![]() 的斜率存在且不为0,设
的斜率存在且不为0,设![]() ,
,
由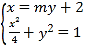 得
得![]() ,∴
,∴![]() ,
,
同理可得![]()
当![]() 时,
时,![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]()
整理得![]() ,所以直线
,所以直线
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,直线也过点
,直线也过点![]()
所以直线![]() 过定点
过定点![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


