题目内容
正数a,b,c满足a+b+c=1,求证:(1-a)(1-b)(1-c)≥8abc。
见解析
证明:∵ a+b+c=1
∴ 1-a=b+c,1-b=a+c,1-c=a=b
∵ a>0,b>0,c>0
∴ b+c≥2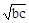 >0
>0
a+c≥2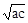 >0
>0
a+b≥2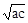 >0
>0
将上面三式相乘得:(b+c)(a+c)(a+b)≥8abc
即(1-a)(1-b)(1-c)≥8abc
∴ 1-a=b+c,1-b=a+c,1-c=a=b
∵ a>0,b>0,c>0
∴ b+c≥2
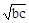 >0
>0a+c≥2
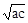 >0
>0a+b≥2
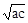 >0
>0将上面三式相乘得:(b+c)(a+c)(a+b)≥8abc
即(1-a)(1-b)(1-c)≥8abc

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
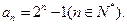 求证:
求证: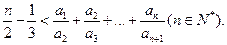
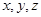 满足
满足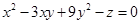 ,则当
,则当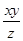 取得最大值时,
取得最大值时,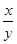 的值为 .
的值为 .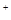 且x+y+z=1,求(
且x+y+z=1,求(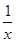 -1)(
-1)( 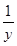 -1)(
-1)( 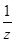 -1)的最小值。
-1)的最小值。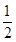 ,2),其横截距与纵截距分别为a、b(a、b均为正数),则使a+b≥c恒成立的c的取值范围为________.
,2),其横截距与纵截距分别为a、b(a、b均为正数),则使a+b≥c恒成立的c的取值范围为________.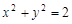 的切线l与两坐标轴分别交于点A,B两点,则
的切线l与两坐标轴分别交于点A,B两点,则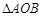 (O为坐标原点)面积的最小值为 .
(O为坐标原点)面积的最小值为 .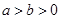 ,则下列不等式正确的是( ).
,则下列不等式正确的是( ).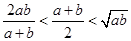
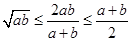
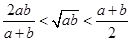
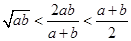
 ,且
,且 ,若
,若 ,则必有
,则必有