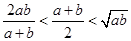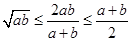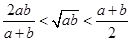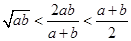题目内容
已知函数f(x)=
(a,b为常数),且方程f(x)-1=0有两个实根为x1=-2,x2=1
(1)求函数f(x)的解析式
(2)设k>1,解关于x的不等式:f(x)<
.
| x2 |
| ax+b |
(1)求函数f(x)的解析式
(2)设k>1,解关于x的不等式:f(x)<
| (k+1)x-k |
| 2-x |
(1)∵函数f(x)=
(a,b为常数),且方程f(x)-1=0有两个实根为x1=-2,x2=1,
∴将x1=-2,x2=1分别代入方程
-1=0,
∴
,解得
,
故f(x)=
(x≠2);
(2)由(1)可知,f(x)=
(x≠2),
∴不等式f(x)<
即为
<
,
整理可得,
<0,
即(x-2)(x-1)(x-k)>0,
①当1<k<2时,不等式的解集为(1,k)∪(2,+∞);
②当k=2时,不等式即为(x-2)2(x-1)>0,
∴不等式的解集为(1,2)∪(2,+∞);
③当k>2时,不等式的解集为(1,2)∪(k,+∞).
综合①②③可得,当1<k<2时,不等式的解集为(1,k)∪(2,+∞),
当k=2时,不等式的解集为(1,2)∪(2,+∞),
当k>2时,不等式的解集为(1,2)∪(k,+∞).
| x2 |
| ax+b |
∴将x1=-2,x2=1分别代入方程
| x2 |
| ax+b |
∴
|
|
故f(x)=
| x2 |
| 2-x |
(2)由(1)可知,f(x)=
| x2 |
| 2-x |
∴不等式f(x)<
| (k+1)x-k |
| 2-x |
| x2 |
| 2-x |
| (k+1)x-k |
| 2-x |
整理可得,
| x2-(k+1)x+k |
| 2-x |
即(x-2)(x-1)(x-k)>0,
①当1<k<2时,不等式的解集为(1,k)∪(2,+∞);
②当k=2时,不等式即为(x-2)2(x-1)>0,
∴不等式的解集为(1,2)∪(2,+∞);
③当k>2时,不等式的解集为(1,2)∪(k,+∞).
综合①②③可得,当1<k<2时,不等式的解集为(1,k)∪(2,+∞),
当k=2时,不等式的解集为(1,2)∪(2,+∞),
当k>2时,不等式的解集为(1,2)∪(k,+∞).

练习册系列答案
相关题目
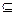 [1,4],求实数a的取值范围?
[1,4],求实数a的取值范围?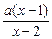 >1(a≠1)。
>1(a≠1)。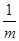 +
+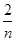 的最小值等于________.
的最小值等于________.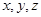 满足
满足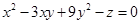 ,则当
,则当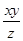 取得最大值时,
取得最大值时,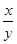 的值为 .
的值为 .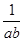 的最小值为( )
的最小值为( )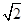
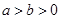 ,则下列不等式正确的是( ).
,则下列不等式正确的是( ).