题目内容
7.已知点P到点A(-2,0)的距离是点P到点B(1,0)的距离的2倍.(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P的坐标为(x,y),求$\frac{y-2}{x-1}$的取值范围;
(Ⅲ)若点P与点Q关于点(2,1)对称,点C(3,0),求|QA|2+|QC|2的最大值和最小值.
分析 (Ⅰ)通过题意,利用两点间距离公式计算即得结论;
(Ⅱ)记K(1,2),通过将$\frac{y-2}{x-1}$视为直线PK的斜率,利用直线与圆的位置关系计算即得结论;
(Ⅲ)通过设Q(2+2cosθ,2+2sinθ),利用两点间距离公式及三角函数的有界性即得结论.
解答 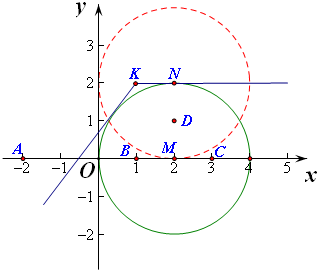 解:(Ⅰ)设点P(x,y),
解:(Ⅰ)设点P(x,y),
∵点P到点A(-2,0)的距离是点P到点B(1,0)的距离的2倍,
∴$\sqrt{(x+2)^{2}+{y}^{2}}$=2$\sqrt{(x-1)^{2}+{y}^{2}}$,即x2+y2-4x=0,
化简可得:(x-2)2+y2=4,
∴点P(x,y)的轨迹是以M(2,0)为圆心,2为半径的圆,
其轨迹方程为:(x-2)2+y2=4;
(Ⅱ)记K(1,2),则$\frac{y-2}{x-1}$可视为直线PK的斜率,
设直线PK的斜率为k,则直线PK的方程为:y-2=k(x-1),
即:kx-y+2-k=0,
由于点K在圆M外,当直线PK与圆M相切时有:$\frac{|2k+2-k|}{\sqrt{1+{k}^{2}}}$=2,
解得:k=0或k=$\frac{4}{3}$,
∴k的取值范围为:k∈[$\frac{4}{3}$,+∞)∪(-∞,0],
∴$\frac{y-2}{x-1}$的取值范围为:(-∞,0]∪[$\frac{4}{3}$,+∞);
(Ⅲ)由题可得,点Q的轨迹是以N(2,2)为圆心,2为半径的圆N,
设Q(2+2cosθ,2+2sinθ),
则|QA|2=(2+2cosθ+2)2+(2+2sinθ)2=24+16cosθ+8sinθ,
|QC|2=(2+2cosθ-3)2+(2+2sinθ)2=9-4cosθ+8sinθ,
∴|QA|2+|QC|2=33+12cosθ+16sinθ=33+20sin(θ+φ),其中tanφ=$\frac{3}{4}$,
当sin(θ+φ)=1时|QA|2+|QC|2取最大值,当sin(θ+φ)=-1时|QA|2+|QC|2取最小值,
∴|QA|2+|QC|2的最大值、最小值分别为:53、13.
点评 本题是一道直线与圆锥曲线的综合题,涉及到直线与圆的位置关系、三角函数有界性、两点间距离公式等基础知识,注意解题方法的积累,属于中档题.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案| A. | 等腰三角形 | B. | 等腰但非直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等边三角形 |
| A. | a≤-1 | B. | -2<a<0 | C. | 0<a<2 | D. | a≥1 |
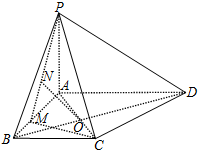 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,其中AD∥BC,BA⊥AD,AC与BD交于点O,M是
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,其中AD∥BC,BA⊥AD,AC与BD交于点O,M是