题目内容
已知数列 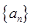 ,
,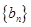 满足
满足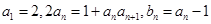 数列
数列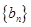 的前
的前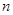 项和为
项和为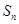 ,
, .
.
(Ⅰ)求数列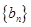 的通项公式;
的通项公式;
(Ⅱ)求证: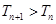 ;
;
(Ⅲ)求证:当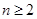 时,
时, .
.
(1)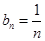
(2)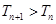
(3)根据题意,利用作差法来比较大小得到证明。
解析试题分析:解:(1)由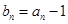 得
得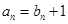 ,代入
,代入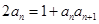

整理得: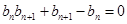 ,从而有
,从而有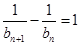 ,
,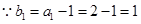
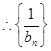 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,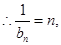 即
即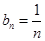 (5分)
(5分)
(2)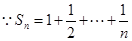
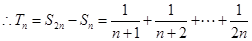
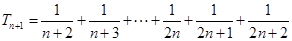
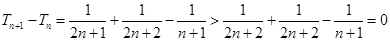
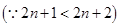
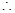
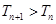 … (10分)
… (10分)
(3)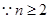
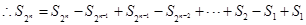
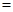
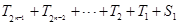
由(2)知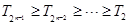 ,
,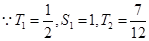
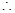
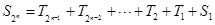
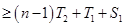
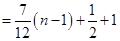
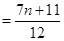 (16分)
(16分)
考点:数列的求和以及通项公式的求解
点评:主要是考查了数列的通项公式与前n项和的关系式的运用,属于中档题。

练习册系列答案
相关题目
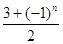 ,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,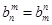 .
. 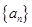 的首项为
的首项为 ,公差为
,公差为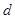 ,且不等式
,且不等式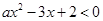 的解集为
的解集为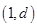 .
.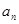 ;
;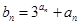 ,求数列
,求数列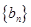 前
前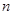 项和
项和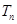 .
.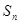 为数列{
为数列{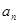 }的前项和,已知
}的前项和,已知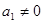 ,2
,2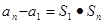 ,
, N
N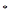
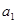 ,
,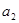 ,并求数列{
,并求数列{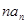 }的前
}的前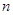 项和。
项和。 的各项均为正数,
的各项均为正数,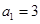 ,前
,前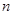 项和为
项和为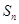 ,等比数列
,等比数列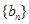 中,
中,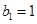 ,
,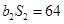 ,
,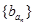 是公比为64的等比数列.
是公比为64的等比数列.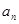 与
与 ;
; 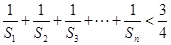 .
.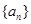 的前n项和为
的前n项和为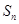 ,已知
,已知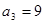 ,
, 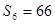 .
.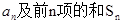 ;
;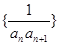 的前n项和为
的前n项和为 ,证明:
,证明: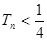 ;
;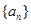 的前
的前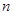 项和
项和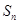 满足
满足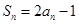 ,等差数列
,等差数列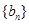 满足
满足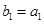 ,
,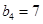 .
.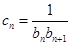 ,数列
,数列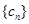 的前
的前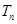 ,求证
,求证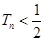 .
.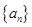 首项
首项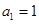 ,公差为
,公差为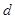 ,且数列
,且数列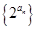 是公比为4的等比数列,
是公比为4的等比数列,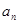 及前
及前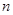 项和
项和 ;
; 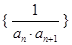 的前
的前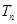 .
.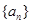 是等差数列,
是等差数列,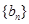 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且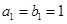 ,
,  ,
,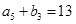
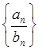 的前n项和
的前n项和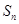 .
.