题目内容
8.若a,b,c为正实数,求证:$\frac{b+c}{a},\frac{a+c}{b},\frac{a+b}{c}$三个数中至少有一个不小于2.分析 假设$\frac{b+c}{a},\frac{a+c}{b},\frac{a+b}{c}$三个数都小于2,因为:a>0,b>0,所以$\frac{b}{a}+\frac{a}{b}≥2$,同理$\frac{c}{a}+\frac{a}{c}≥2,\frac{b}{c}+\frac{c}{b}≥2$,相加可$\frac{b}{a}+\frac{a}{b}+\frac{c}{a}+\frac{a}{c}+\frac{b}{c}+\frac{c}{b}≥6$,再结合$\frac{b+c}{a}+\frac{a+c}{b}+\frac{a+b}{c}<6$,引出矛盾,即可得出结论.
解答 证明:假设$\frac{b+c}{a},\frac{a+c}{b},\frac{a+b}{c}$三个数都小于2…(2分)
因为:a>0,b>0,所以$\frac{b}{a}+\frac{a}{b}≥2$,
同理$\frac{c}{a}+\frac{a}{c}≥2,\frac{b}{c}+\frac{c}{b}≥2$
又$\frac{b+c}{a}+\frac{a+c}{b}+\frac{a+b}{c}=\frac{b}{a}+\frac{a}{b}+\frac{c}{a}+\frac{a}{c}+\frac{b}{c}+\frac{c}{b}$,
所以$\frac{b}{a}+\frac{a}{b}+\frac{c}{a}+\frac{a}{c}+\frac{b}{c}+\frac{c}{b}≥6$…(6分)
由题设可知$\frac{b+c}{a}<2,\frac{a+c}{b}<2,\frac{a+b}{c}<2$
所以$\frac{b+c}{a}+\frac{a+c}{b}+\frac{a+b}{c}<6$…(10分)
这与$\frac{b}{a}+\frac{a}{b}+\frac{c}{a}+\frac{a}{c}+\frac{b}{c}+\frac{c}{b}≥6$相矛盾,
故假设不成立,
所以$\frac{b+c}{a},\frac{a+c}{b},\frac{a+b}{c}$三个数中至少有一个不小于2…(12分)
点评 用反证法证明数学命题的方法和步骤,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,属于中档题.

 53随堂测系列答案
53随堂测系列答案| A. | $(1,1+\sqrt{7})$ | B. | $(1,2+\sqrt{7})$ | C. | $(3,1+\sqrt{7})$ | D. | (3,2+$\sqrt{7}$) |
| A. | 100 | B. | 120 | C. | 160 | D. | 200 |
| A. | $\frac{f(m-{m}^{2})}{{e}^{{m}^{2}-m+1}}$>f(1) | B. | $\frac{f(m-{m}^{2})}{{e}^{{m}^{2}-m+1}}$<f(1) | ||
| C. | $\frac{f(m-{m}^{2})}{{e}^{{m}^{2}-m+1}}$≥f(1) | D. | $\frac{f(m-{m}^{2})}{{e}^{{m}^{2}-m+1}}$≤f(1) |
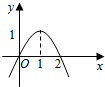 已知f(x)=ax3+bx2+c,其导函数f′(x)的图象如图所示,则函数f(x)取得极小值时x的值是0.
已知f(x)=ax3+bx2+c,其导函数f′(x)的图象如图所示,则函数f(x)取得极小值时x的值是0.