题目内容
10.已知数列{an}的前n项和为Sn=$\frac{1}{4}$n2+$\frac{2}{3}$n+3,求这个数列的通项公式.分析 根据数列项和前n项和之间的关系进行求解即可.
解答 解:(1)当n=1时,a1=S1=$\frac{47}{12}$,
(2)当n≥2时,an=Sn-Sn-1=$\frac{1}{4}$n2+$\frac{2}{3}$n+3-[$\frac{1}{4}$(n-1)2+$\frac{2}{3}$(n-1)+3]=$\frac{1}{2}$n+$\frac{5}{12}$.
经检验,a1=$\frac{47}{12}$,不满足上式.
所以这个数列的通项公式an=$\left\{\begin{array}{l}{\frac{47}{12},n=1}\\{\frac{1}{2}n+\frac{5}{12},n≥2}\end{array}\right.$.
点评 本题主要考查数列通项公式的求解,根据an=Sn-Sn-1的关系是解决本题的关键.

练习册系列答案
相关题目
5.若a,b∈R且a≠b,则在 ①a+b>2b2; ②a5+b5>a3b2+a2b3;③a2+b2≥2(a-b-1); ④$\frac{b}{a}$+$\frac{a}{b}$>2.这四个式子中一定成立的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.已知全集U={0,1,2,3,4,5,6,7,8},集合A={0,1,3,5,8},集合B={2,4,5,6,8},则(∁UA)∩(∁UB)=( )
| A. | {5,8} | B. | {7} | C. | {0,1,3} | D. | {2,4,6} |
19.已知△AOB的顶点坐标分别是A(4,0),B(0,3),O(0,0)则△AOB外接圆的方程是( )
| A. | x2+y2+4x-3y=0 | B. | x2+y2-4x-3y=0 | C. | x2+y2+4x+3y=0 | D. | x2+y2-4x+3y=0 |
20.双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$的焦距为( )
| A. | $3\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | $4\sqrt{5}$ |
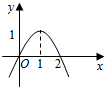 已知f(x)=ax3+bx2+c,其导函数f′(x)的图象如图所示,则函数f(x)取得极小值时x的值是0.
已知f(x)=ax3+bx2+c,其导函数f′(x)的图象如图所示,则函数f(x)取得极小值时x的值是0.