题目内容
15．设△ABC中，a=1，b=2，cosC=$\frac{1}{4}$，则sinB=$\frac{{\sqrt{15}}}{4}$．分析 根据余弦定理，正弦定理进行求解即可．
解答 解：由余弦定理得c2=a2+b2-2abcosC=1+4-2×$1×2×\frac{1}{4}$=4，
即c=2，
则cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1+4-4}{2×1×2}$=$\frac{1}{4}$，
则sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{{\sqrt{15}}}{4}$，
故答案为：$\frac{{\sqrt{15}}}{4}$
点评 本题主要考查解三角形的应用，根据余弦定理是解决本题的关键．
练习册系列答案
相关题目
5．“ac=bc”是“a=b”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
6．已知$x∈（{-\frac{π}{2}，\frac{π}{2}}），sinx+cosx=\frac{1}{5}$，则tan2x为（ ）
| A． | $\frac{7}{24}$ | B． | $-\frac{7}{24}$ | C． | $\frac{24}{7}$ | D． | $-\frac{24}{7}$ |
3．将一个三位数的三个数字顺序颠倒，将所得到的数与原数相加，若和中没有一个数字是偶数，则称这个数为“奇和数”．那么，所有的三位数中，奇和数有（ ）个．
| A． | 100 | B． | 120 | C． | 160 | D． | 200 |
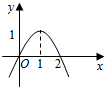已知f（x）=ax3+bx2+c，其导函数f′（x）的图象如图所示，则函数f（x）取得极小值时x的值是0．