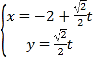题目内容
【题目】已知函数![]() .(其中
.(其中![]() 为自然对数的底数)
为自然对数的底数)
(1)若![]() 恒成立,求
恒成立,求![]() 的最大值;
的最大值;
(2)设![]() ,若
,若![]() 存在唯一的零点,且对满足条件的
存在唯一的零点,且对满足条件的![]() 不等式
不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值集合.
的取值集合.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)就![]() 三种情况利用导数讨论
三种情况利用导数讨论![]() 的单调性及其相应的最小值后可得:
的单调性及其相应的最小值后可得:![]() 时,
时,![]() 成立,
成立,![]() 时,
时,![]() 成立,对后一种情况构建新函数
成立,对后一种情况构建新函数![]() ,利用导数可求
,利用导数可求![]() 的最大值即可.
的最大值即可.
(2)求出![]() ,它是一个减函数且值域
,它是一个减函数且值域![]() ,故
,故![]() 存在唯一的零点
存在唯一的零点![]() ,再由题设条件可以得到
,再由题设条件可以得到![]() ,
,![]() ,用
,用![]() 表示
表示![]() 后可把不等式
后可把不等式![]() 化为
化为![]() ,构建新函数
,构建新函数![]() ,就
,就![]() 两类情况利用导数讨论函数的单调性后可得实数
两类情况利用导数讨论函数的单调性后可得实数![]() 的取值,注意后者的进一步讨论以
的取值,注意后者的进一步讨论以![]() 与
与![]() 的大小为分类标准.
的大小为分类标准.
(1)![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,取
上单调递增,取![]() ,
,
当![]() 时,
时,![]() 矛盾;
矛盾;
当![]() 时,
时,![]() ,
,
只要![]() ,即
,即![]() ,此时
,此时![]() ;
;
当![]() 时,令
时,令![]() ,
,![]() ,
,
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
![]() ,
,
所以![]() ,即
,即![]() ,
,
此时![]() ,
,
令![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
当![]() ,
,![]() ,
,![]() 在
在![]() 上为增函数;
上为增函数;
当![]() ,
,![]() ,
,![]() 在
在![]() 上为减函数.
上为减函数.
所以![]() ,所以
,所以![]() ,故
,故![]() 的最大值为
的最大值为![]() .
.
(2)![]() 在
在![]() 单调递减且
单调递减且![]() 在
在![]() 的值域为
的值域为![]() ,
,
设![]() 的唯一的零点为
的唯一的零点为![]() ,则
,则![]() ,
,![]() ,
,
即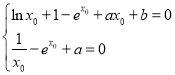
所以![]() ,
,![]() ,
,
由![]() 恒成立,则
恒成立,则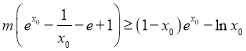 ,
,
得![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,
,![]() ,
,
![]() .
.
若![]() ,
,![]() ,
,![]() 在
在![]() 上为增函数,注意到
上为增函数,注意到![]() ,知当
,知当![]() 时,
时,![]() ,矛盾;
,矛盾;
当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
若![]() ,则当
,则当![]() 时,
时,![]() ,,
,,![]() 为减函数,
为减函数,
所以![]() 时,总有
时,总有![]() ,矛盾;
,矛盾;
若![]() ,则当
,则当![]() 时,
时,![]() ,,
,,![]() 为增函数,
为增函数,
所以![]() 时,总有
时,总有![]() ,矛盾;
,矛盾;
所以![]() 即
即![]() ,此时当
,此时当![]() 时,
时,![]() ,
,![]() 为增函数,,
为增函数,,
当![]() 时,
时,![]() ,
,![]() 为减函数,而
为减函数,而![]() ,
,
所以![]() 有唯一的零点.
有唯一的零点.
综上,![]() 的取值集合为
的取值集合为![]() .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目