题目内容
17.通过圆与球的类比,由“半径为R的圆的内接矩形中,以正方形的面积为最大,最大值为2R2”,猜想关于球的相应命题为( )| A. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为2R3 | |
| B. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为3R3 | |
| C. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为$\frac{4\sqrt{3}}{9}$R3 | |
| D. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为$\frac{8\sqrt{3}}{9}$R3 |
分析 在由平面几何的性质类比推理空间立体几何性质时,我们常用的思路是:由平面几何中点的性质,类比推理空间几何中线的性质;由平面几何中线的性质,类比推理空间几何中面的性质;由平面几何中面的性质,类比推理空间几何中体的性质;故由:周长一定的所有矩形中,正方形的面积最大”,类比到空间可得的结论是表面积一定的所有长方体中,正方体的体积最大.
解答 解:在由平面几何的性质类比推理空间立体几何性质时,
一般为:由平面几何中点的性质,类比推理空间几何中线的性质;
由平面几何中线的性质,类比推理空间几何中面的性质;
由平面几何中面的性质,类比推理空间几何中体的性质;
故由:“周长一定的所有矩形中,正方形的面积最大”,
类比到空间可得的结论是:
“半径为R的球的内接长方体中以正方体的体积为最大,最大值为$\frac{8\sqrt{3}}{9}$R3.”
故选:D.
点评 类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
18.已知函数f(x)是R奇函数,在(0,+∞)是增函数且f(1)=0,则f(log2a)>0的a的取值范围是( )
| A. | $\frac{1}{2}$<a<1或a>2 | B. | 0$<a<\frac{1}{2}$ | C. | 0$<a<\frac{1}{2}$或a>2 | D. | a>2 |
9.如图,该程序运行后输出的结果为是( )
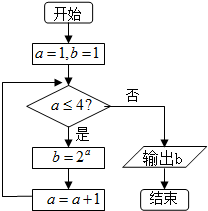

| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
6.如果执行下面的程序框图,输出的S=240,则判断框中为( )


| A. | k≥15? | B. | k≤16? | C. | k≤15? | D. | k≥16? |
7.给出一个程序框图,则输出x的值是( )


| A. | 39 | B. | 41 | C. | 43 | D. | 45 |