题目内容
【题目】已知f(x)=|x2﹣2x﹣3|
(1)求f(x)的单调区间;
(2)若g(x)=f(x)﹣m有4个零点,求m的取值范围.
【答案】
(1)解:令f(x)=|x2﹣2x﹣3|=0,解得x=﹣1或x=3,
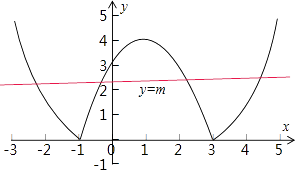
画出函数f(x)=|x2﹣2x﹣3|=|(x﹣1)2﹣4|的图象:
由图得,
f(x)的增区间是(﹣1,1),(3,+∞),
减区间是(﹣∞,﹣1),(1,3)
(2)解:∵g(x)=f(x)﹣m有4个零点,
∴函数y=f(x)的图象与直线y=m有4个不同的交点,
由图得,m的取值范围是(0,4).
【解析】(1)求出方程f(x)=0的根,利用配方法化简后,由二次函数的图象画出f(x)的函数图象,由图象写出f(x)的单调区间;(2)将函数g(x)的零点问题转化为函数图象的交点问题,由图求出m的取值范围.

练习册系列答案
相关题目



