Question

【题目】如图，小华和小明两个小伙伴在一起做游戏，他们通过划拳（剪刀、石头、布）比赛决胜谁首先登上第3个台阶，他们规定从平地开始，每次划拳赢的一方登上一级台阶，输的一方原地不动，平局时两个人都上一级台阶，如果一方连续两次赢，那么他将额外获得一次上一级台阶的奖励，除非已经登上第3个台阶，当有任何一方登上第3个台阶时，游戏结束，记此时两个小伙伴划拳的次数为．

（1）求游戏结束时小华在第2个台阶的概率；

（2）求的分布列和数学期望．

Answer 1

【答案】（1）（2）

【解析】试题分析：（1）根据等可能性知每次赢、平、输的概率皆为．再分两种情况分别计数：一种是小华在第1个台阶，并且小明在第2个台阶，最后一次划拳小华平；另一种是小华在第2个台阶，并且小明也在第2个台阶，最后一次划拳小华输，逆推确定事件数及对应划拳的次数，最后利用互斥事件概率加法公式求概率，（2）先确定随机变量取法,再分别利用组合求对应概率,列表可得分布列,最后根据数学期望公式求期望.

试题解析：解：（1）易知对于每次划拳比赛基本事件共有个，其中小华赢（或输）包含三个基本事件上，他们平局也为三个基本事件，不妨设事件“第次划拳小华赢”为；事件“第 次划拳小华平”为；事件“第 次划拳小华输”为，所以．

因为游戏结束时小华在第2个台阶，所以这包含两种可能的情况：

第一种：小华在第1个台阶，并且小明在第2个台阶，最后一次划拳小华平；

其概率为，

第二种：小华在第2个台阶，并且小明也在第2个台阶，最后一次划拳小华输，

其概率为

所以游戏结束时小华在第2个台阶的概率为．

（2）依题可知的可能取值为2、3、4、5，

，

，

，

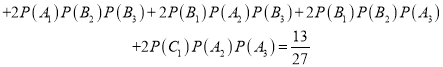
所以的分布列为：

	2	3	4	5

所以的数学期望为：

．