题目内容
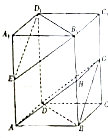
12.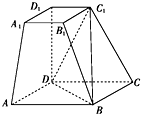 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°.(1)证明:BD⊥AA1;
(2)证明:AA1∥平面BC1D.
分析 (1)由已知条件利用余弦定理得BD2=AD2,从而利用勾股定理得AD⊥BD,进而得到BD⊥平面ADD1A1,由此能证明BD⊥AA1.
(2)连结AC、A1C1,设AC∩BD=E,连结EC1,由棱台的定义结合已知条件推导出四边形A1C1EA是平行四边形,由此能证明AA1∥平面BC1D.
解答 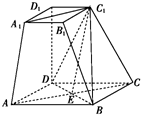 证明:(1)∵AB=$\sqrt{2}$AD,∠BAD=45°,
证明:(1)∵AB=$\sqrt{2}$AD,∠BAD=45°,
在△ABD中,由余弦定理得BD2=AD2+AB2-2AD•ABcos 45°=AD2,
∴AD2+BD2=AB2,∴AD⊥BD,
∵DD1⊥平面ABCD,且BD?平面ABCD,
∴DD1⊥BD,又AD∩DD1=D,∴BD⊥平面ADD1A1.
又AA1?平面ADD1A1,∴BD⊥AA1.(7分)
(2)连结AC、A1C1,设AC∩BD=E,连结EC1,
∵四边形ABCD是平行四边形,∴AE=$\frac{1}{2}$AC,
由棱台的定义及AB=$\sqrt{2}$AD=2A1B1知,A1C1∥AE,且A1C1=AE,
∴四边形A1C1EA是平行四边形,∴AA1∥EC1,
又∵EC1?平面BC1D,AA1?平面BC1D,
∴AA1∥平面BC1D.(14分)
点评 本题考查异面直线垂直的证明,考查线面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
2.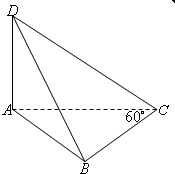 如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
 如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
20.已知随机变量X服从正态分布N(2,σ2),P(X≤3)=0.72,则P(1<X<3)等于( )
| A. | 0.28 | B. | 0.44 | C. | 0.56 | D. | 0.84 |
17.若sinα=-$\frac{3}{5}$,α是第三象限的角,则$\frac{cos\frac{α}{2}+sin\frac{α}{2}}{cos\frac{α}{2}-sin\frac{α}{2}}$等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
4.已知数列{an}为等差数列,若a3+a7=20,则数列{an}的前9项和S9等于( )
| A. | 40 | B. | 45 | C. | 60 | D. | 90 |
 如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.
如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.