题目内容
△ABC的三个内角A,B,C的对边分别a,b,c,且acos C,bcos B,ccos A成等差数列,则角B等于( )
| A.30° | B.60° | C.90° | D.120° |
B
由题意,得2bcos B=acos C+ccos A,根据正弦定理可得2sin Bcos B=sin Acos C+cos Asin C,即2sin Bcos B=sin(A+C)=sin B,解得cos B= ,所以B=60°
,所以B=60°
 ,所以B=60°
,所以B=60°
练习册系列答案
相关题目
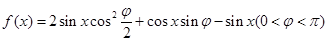 在
在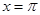 处取最小值.
处取最小值.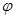 的值。
的值。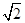 ,
,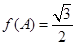 ,求角C.
,求角C.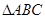 的内角
的内角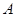 ,
,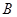 ,
,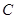 所对的边长分别为
所对的边长分别为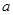 ,
,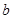 ,
,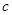 ,且
,且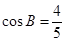 ,
,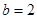 .
.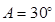 时,求
时,求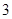 时,求
时,求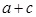 的值.
的值. ,
,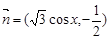 ,函数
,函数 .
. 的最大值,并求取最大值时
的最大值,并求取最大值时 的取值集合;
的取值集合;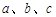 分别为
分别为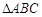 内角
内角 的对边,且
的对边,且 为锐角,且
为锐角,且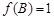 ,求
,求 的值.
的值.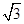 b.
b.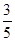 ,cos B=
,cos B=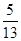 ,b=3,则c=________.
,b=3,则c=________.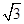 b,则角A等于________.
b,则角A等于________.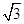 ,则c= ( ).
,则c= ( ).