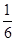题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c且cos A=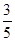 ,cos B=
,cos B=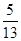 ,b=3,则c=________.
,b=3,则c=________.
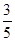 ,cos B=
,cos B=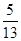 ,b=3,则c=________.
,b=3,则c=________.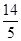
因为cos A=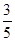 ,cos B=
,cos B=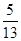 ,所以sin A=
,所以sin A=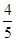 ,
,
sin B=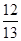 .由正弦定理得
.由正弦定理得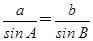 ,即
,即 ,所以a=
,所以a= .由余弦定理得b2=a2+c2-2accos B,即9=
.由余弦定理得b2=a2+c2-2accos B,即9=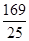 +c2-2c,解得c=
+c2-2c,解得c=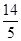 (负值舍去).
(负值舍去).
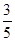 ,cos B=
,cos B=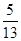 ,所以sin A=
,所以sin A=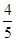 ,
,sin B=
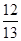 .由正弦定理得
.由正弦定理得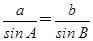 ,即
,即 ,所以a=
,所以a= .由余弦定理得b2=a2+c2-2accos B,即9=
.由余弦定理得b2=a2+c2-2accos B,即9=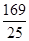 +c2-2c,解得c=
+c2-2c,解得c=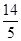 (负值舍去).
(负值舍去).
练习册系列答案
相关题目
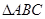 的内角
的内角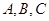 所对的边分别为
所对的边分别为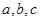 ,且有
,且有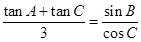 .
.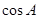 的值;
的值;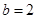 ,
,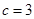 ,
,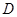 为
为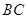 上一点.且
上一点.且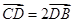 ,求
,求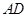 的长.
的长.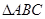 中,角
中,角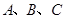 所对边分别为
所对边分别为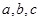 ,已知
,已知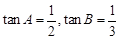 ,且最长边的边长为
,且最长边的边长为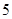 .求:
.求: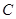 的正切值及其大小;
的正切值及其大小;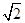 ,点M在线段PQ上.
,点M在线段PQ上.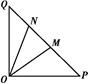
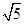 ,求PM的长;
,求PM的长; b,sin B=sin C,则B等于________.
b,sin B=sin C,则B等于________.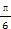 ,AC=1,AB=
,AC=1,AB=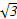 ,则BC的长为 .
,则BC的长为 .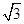 ,∠C=
,∠C=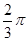 ,则△ABC的面积为________.
,则△ABC的面积为________.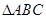 中,角A.B.C所对的边分别是
中,角A.B.C所对的边分别是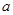 .
.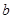 .
.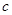 ,若
,若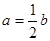 ,
,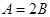 ,则
,则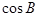 等于( )
等于( )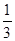 B.
B.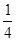 C.
C.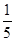 D.
D.