题目内容
(本小题满分14分)
已知二次函数 ,且不等式
,且不等式 的解集为
的解集为 。
。
(Ⅰ) 若方程 有两个相等的实根,求
有两个相等的实根,求 的解析式;
的解析式;
(Ⅱ) 若函数 的最小值不大于
的最小值不大于 ,求实数
,求实数 的取值范围。
的取值范围。
(Ⅲ)  如何取值时,函数
如何取值时,函数 (
( )存在零点,并求出零点.
)存在零点,并求出零点.
解:∵ 的解集为
的解集为 ,
,
∴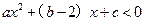 的解集为
的解集为 ,
,
∴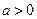 ,且方程
,且方程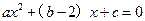 的两根为
的两根为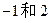
即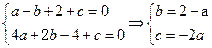
∴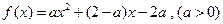
(Ⅰ)∵方程 有两个相等的实根,
有两个相等的实根,
即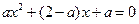 有两个相等的实根
有两个相等的实根
∴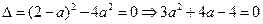 ,∴
,∴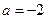 或
或
∵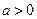 ,∴
,∴ , ∴
, ∴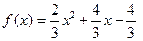
(Ⅱ)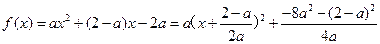
∵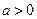 ,∴
,∴ 的最小值为
的最小值为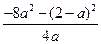 ,则
,则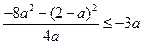
∴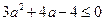 ,解得
,解得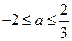 , ∵
, ∵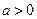 ,∴
,∴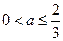
(Ⅲ)由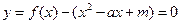 ,得
,得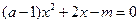 (※)
(※)
①当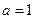 时,方程(※)有一解
时,方程(※)有一解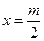 ,函数
,函数 有一零点
有一零点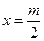 ;
;
②当 且
且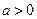 时,方程(※)有二解
时,方程(※)有二解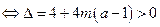 ,
,
i)若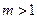 ,
,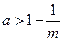
函数 有两个零点
有两个零点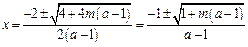 ;
;
ii) 若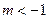 ,
, ,函数
,函数 有两个零点
有两个零点 ;
;
③当 时,方程(※)有一解
时,方程(※)有一解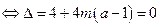 ,
, 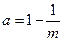 , 函数
, 函数 有一零点
有一零点 .
.
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
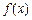 满足
满足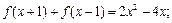
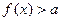 在
在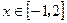 上恒成立,求实数
上恒成立,求实数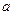 的取值范围;
的取值范围;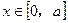 (
(
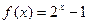 的反函数为
的反函数为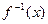 ,
,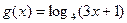 .
.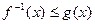 ,求
,求 的取值范围D;
的取值范围D;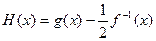 ,当
,当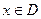 时,求函数
时,求函数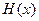 的值域.
的值域. 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 时,有
时,有
 .
. ;
; 对所有
对所有 恒成立,求实数
恒成立,求实数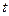 的取值范围.
的取值范围.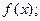
 的图像与
的图像与 轴的交点至少有一个在原点的右侧,求实数
轴的交点至少有一个在原点的右侧,求实数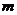 的取值范围。
的取值范围。 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数, 的图象与
的图象与 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时, 222233.
222233. 上为增函数,求
上为增函数,求 的取值范围;
的取值范围; 上?若存在,求出
上?若存在,求出
 的极值;
的极值; 若函数
若函数 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数  的取值范围.
的取值范围.