题目内容
已知二次函数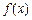 满足
满足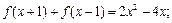
(1)求函数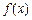 的解析式 ;
的解析式 ;
(2)若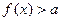 在
在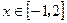 上恒成立,求实数
上恒成立,求实数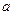 的取值范围;
的取值范围;
(3)求当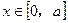 (
(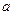 >0)时
>0)时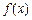 的最大值
的最大值
(1)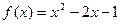
⑵ 在
在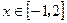 上的最小值为
上的最小值为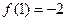
∴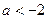
⑶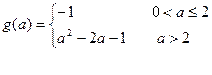
解析

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
题目内容
已知二次函数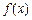 满足
满足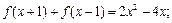
(1)求函数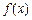 的解析式 ;
的解析式 ;
(2)若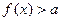 在
在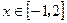 上恒成立,求实数
上恒成立,求实数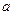 的取值范围;
的取值范围;
(3)求当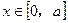 (
(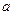 >0)时
>0)时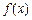 的最大值
的最大值
(1)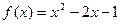
⑵ 在
在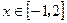 上的最小值为
上的最小值为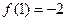
∴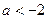
⑶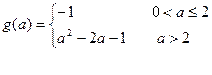
解析

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案