题目内容

5．已知等差数列{an}的公差不为零，若a1、a2、a6成等比数列且和为21，则数列{an}的通项公式为（　　）
A．an=3n+1B．an=3nC．an=3n-2D．an=3n-5

分析 等差数列{an}的公差不为零，设为d，根据a1、a2、a6成等比数列，且和为21，求出a1与d的值，即可确定出通项公式．

解答 解：∵等差数列{an}的公差不为零，设为d，
∴a2=a1+d，a6=a1+5d，
∵a1、a2、a6成等比数列，且和为21，
∴a22=a1•a6，a1+a2+a6=21，
即（a1+d）2=a1（a1+5d），3a1+d+5d=21，
解得：a1=1，d=3，
则数列{an}的通项公式为an=3n-2，
故选：C．

点评 此题考查了等差数列的通项公式，熟练掌握等差数列的性质是解本题的关键．

练习册系列答案
相关题目
15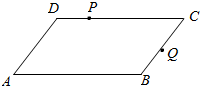．如图在平行四边形ABCD中，已知AB=3，AD=2，∠DAB=60°，2$\overrightarrow{DP}$=$\overrightarrow{PC}$，$\overrightarrow{BQ}$=$\overrightarrow{QC}$，则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=（　　）
A．$\frac{13}{2}$B．$\frac{15}{2}$C．$\frac{17}{2}$D．$\frac{19}{2}$
16．有学生若干人，住若干宿舍，如果每间住4人，那么还余19人；如果每间住6人，那么有一间不满也不空，则宿舍间数及学生人数分别为10，59或11，63或12，67．
13．已知函数f（x）=2$\sqrt{3}sin（x+\frac{π}{4}）cos（x+\frac{π}{4}）+sin2x+a$的最大值为1．
（Ⅰ）求常数a的值；
（Ⅱ）求函数f（x）的单调递增区间．
20．在（x2+3x+2）5的展开式中x的系数为（　　）
A．800B．360C．240D．160
10．为了得到函数y=2sin（2x-$\frac{π}{6}$）的图象，可以将y=2sin（2x+$\frac{π}{6}$）的图象（　　）
A．向右平移$\frac{π}{6}$个单位B．向左平移$\frac{π}{6}$个单位
C．向右平移$\frac{π}{3}$个单位D．向左平移$\frac{π}{3}$个单位
17．设函数f（x）是定义在（-∞，0）上的可导函数，其导函数为f′（x），且有2f（x）+xf′（x）＞x2，则不等式（x+2015）2f（x+2015）-4f（-2）＞0的解集为（　　）
A．（-2016，0）B．（-2012，0）C．（-∞，-2016）D．（-∞，-2017）
14．对于任意实数x，[x]表示x的整数部分，即[x]是不超过x的最大整数，这个函数[x]叫做“取整函数”则[lg1]+[lg2]+[lg3]+…+[lg2010]=4923．
15．若函数f（x）=1ogax（0＜a＜1）在区间[a，3a]上的最大值是最小值的2倍，则a=（　　）
A．$\frac{2}{3}$B．$\frac{\sqrt{3}}{3}$C．$\frac{1}{3}$D．$\frac{1}{9}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网