题目内容
17.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x+2015)2f(x+2015)-4f(-2)>0的解集为( )| A. | (-2016,0) | B. | (-2012,0) | C. | (-∞,-2016) | D. | (-∞,-2017) |
分析 令g(x)=x2f(x),求导g′(x)=x2f′(x)+2xf(x)=x(xf′(x)+2f(x)),从而可得g(x)在(-∞,0)上是减函数,从而解得.
解答 解:令g(x)=x2f(x),
g′(x)=x2f′(x)+2xf(x)=x(xf′(x)+2f(x)),
∵2f(x)+xf′(x)>x2>0,x<0;
∴x(xf′(x)+2f(x))<0,
∴g(x)=x2f(x)在(-∞,0)上是减函数,
∴(x+2015)2f(x+2015)-4f(-2)>0可化为
(x+2015)2f(x+2015)>4f(-2)=(-2)2f(-2),
∴x+2015<-2,
故x<-2017;
故选D.
点评 本题考查了导数的综合应用及单调性的应用.

练习册系列答案
相关题目
8.已知a,b是实数,命题p:“a+b>5”,命题q:“$\left\{\begin{array}{l}{a>2}\\{b>3}\end{array}\right.$”,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
5.已知等差数列{an}的公差不为零,若a1、a2、a6成等比数列且和为21,则数列{an}的通项公式为( )
| A. | an=3n+1 | B. | an=3n | C. | an=3n-2 | D. | an=3n-5 |
12.复数z满足(1+i)z=2i(i为虚数单位),则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.设全集为U,A⊆U,B⊆U,则“A∩B=φ”是“A⊆∁UB”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
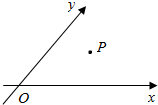 如图,设α∈(0,π)且$α≠\frac{π}{2}$,当∠xOy=α时,定义平面坐标系xOy为斜坐标系,在斜坐标系中,任意一点P的斜坐标这样定义:e1,e2分别为x轴、y轴正方向相同的单位向量,若$\overrightarrow{OP}=x{e_1}+y{e_2}$,则记为$\overrightarrow{OP}=(x,y)$,那么在以下的结论中,正确的有(2)(4)(填上所有正确结论的序号).
如图,设α∈(0,π)且$α≠\frac{π}{2}$,当∠xOy=α时,定义平面坐标系xOy为斜坐标系,在斜坐标系中,任意一点P的斜坐标这样定义:e1,e2分别为x轴、y轴正方向相同的单位向量,若$\overrightarrow{OP}=x{e_1}+y{e_2}$,则记为$\overrightarrow{OP}=(x,y)$,那么在以下的结论中,正确的有(2)(4)(填上所有正确结论的序号).