题目内容

14．对于任意实数x，[x]表示x的整数部分，即[x]是不超过x的最大整数，这个函数[x]叫做“取整函数”则[lg1]+[lg2]+[lg3]+…+[lg2010]=4923．

分析 由于[lg1]=[lg2]=[lg3]=[lg4]=…=[lg9]=0，有9个0；[lg10]=[lg11]=…[lg99]=1，有90个1；[lg100]=[lg101]=…=[lg999]=2，有900个2；[lg1000]=[lg1001]=…=[lg2010]=3，有1011个3，代入可求和可得答案．

解答 解：∵[lg1]=[lg2]=[lg3]=[lg4]=…=[lg9]=0，有9个0
[lg10]=[lg11]=…[lg99]=1，有90个1
[lg100]=[lg101]=…=[lg999]=2，有900个2
[lg1000]=[lg1001]=…=[lg2010]=3，有1011个3
则[lg1]+[lg2]+[lg3]+[lg4]+…+[lg2009]=9×0+90×1+990×2+1011×3=4923
故答案为：4923．

点评 本题以新定义为载体，主要考查了对数函数值的基本运算，解题的关键：是对对数值准确取整的计算与理解．

练习册系列答案
相关题目
4．已知下列四个命题：
①若函数y=f（x）在定义域上为减函数，则函数y=-f（x）在定义域上为增函数；
②若函数y=f（x）在定义域上为增函数，则函数g（x）=$\frac{1}{f（x）}$在其定义域内为减函数；
③若函数y=1+loga（x-1）图象过定点P（m，n），则logmn=0；
④若函数y=f（x）和y=g（x）在区间[-a，a]上都是奇函数，则函数y=f（x）•g（x）在区间[-a，a]上是偶函数，其中正确命题的序号是①④．
5．已知等差数列{an}的公差不为零，若a1、a2、a6成等比数列且和为21，则数列{an}的通项公式为（　　）
A．an=3n+1B．an=3nC．an=3n-2D．an=3n-5
2．设全集为U，A⊆U，B⊆U，则“A∩B=φ”是“A⊆∁UB”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
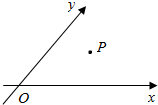9．如图，设α∈（0，π）且$α≠\frac{π}{2}$，当∠xOy=α时，定义平面坐标系xOy为斜坐标系，在斜坐标系中，任意一点P的斜坐标这样定义：e1，e2分别为x轴、y轴正方向相同的单位向量，若$\overrightarrow{OP}=x{e_1}+y{e_2}$，则记为$\overrightarrow{OP}=（x，y）$，那么在以下的结论中，正确的有（2）（4）（填上所有正确结论的序号）．
（1）设a=（m，n），则$|a|=\sqrt{{m^2}+{n^2}}$；
（2）设a=（m，n），b=（s，t），若a=b，则m=s，n=t；
（3）设a=（m，n），b=（s，t），若a⊥b，则ms+nt=0；
（4）设a=（m，n），b=（s，t），若a∥b，则mt-ns=0．
19．已知函数f（x）=$\left\{\begin{array}{l}{{3}^{-x}-1（x≤0）}\\{\sqrt{x}（x＞0）}\end{array}\right.$，若函数g（x）=f（x）-$\frac{1}{2}$x-b有三个零点，则实数b的取值范围是（0，$\frac{1}{2}$）．
6．已知函数f（x）=x2+$\frac{a}{2}$lnx．
（1）求f（x）的单调区间；
（2）是否存在实数a，使f（x）在（0，1]上的最小值是0，若存在，求实数a的值，若不存在，说明理由；
（3）已知g（x）=ax（x∈（0，1]），当a＜0时，对于任意的x1∈（0，+∞），存在x2∈（0，1]，使得f（x1）≥g（x2），求实数a的取值范围．
3．斜率为k（k＞0）的直线l与抛物线C：y2=4x交于A，B两点，O为原点，M是线段AB的中点，F为C的焦点，△OFM的面积等于2，则k=$\frac{1}{2}$．
4．设二次函数y=f（x）的最大值为9，且f（3）=f（-1）=5，
（1）求f（x）的解析式；
（2）求f（x）在[0，4]上的最值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网