题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,
时,![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时,![]() 在
在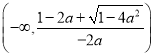 ,
,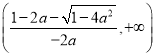 上单调递减,在
上单调递减,在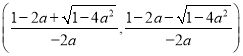 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减(Ⅱ)
上单调递减(Ⅱ)![]() .
.
【解析】
(Ⅰ)求出导函数![]() ,令
,令![]() ,只需
,只需![]() ,由
,由![]() ,讨论
,讨论![]() 的取值范围,根据导数与函数单调性的关系即可求解.
的取值范围,根据导数与函数单调性的关系即可求解.
(Ⅱ)将不等式转化为![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,求出
,求出![]() ,讨论
,讨论![]() 的取值范围,当
的取值范围,当![]() 时,令
时,令![]() ,利用导数研究
,利用导数研究![]() 的单调性,确定
的单调性,确定![]() 的符号,进而可到
的符号,进而可到![]() 的单调性,根据单调性即可求解.
的单调性,根据单调性即可求解.
(Ⅰ)![]()
![]() ,
,
令![]() ,即
,即![]() ,
,![]() ,
,
∵![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
∴![]() 在
在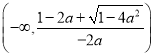 ,
,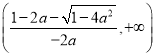 上单调递减,
上单调递减,
在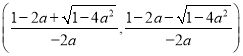 上单调递增;
上单调递增;
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
(Ⅱ)当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则
,则![]() ,
,
当![]() 时,在
时,在![]() 上,都有
上,都有![]() ,
,![]() ,
,
即![]() 恒成立,与题意矛盾;
恒成立,与题意矛盾;
当![]() 时,令
时,令![]() ,
,![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
①若![]() ,即
,即![]() ,
,![]() 时,
时,![]() ,
,
∴![]() ,
,![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() 成立,
成立,
②当![]() ,即
,即![]() ,
,![]() ,
,
∴存在![]() 使得
使得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 在
在![]() 单调递增,∴存在
单调递增,∴存在![]() 使得
使得![]() 与题意矛盾,
与题意矛盾,
综上所述![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】闰月年指农历里有闰月的年份,比如2020年是闰月年,4月23日至5月22日为农历四月,5月23日至6月20日为农历闰四月.农历置闰月是为了农历年的平均长度接近回归年:农历年中的朔望月的平均长度为29.5306日,![]() 日,回归年的总长度为365.2422日,两者相差10.875日.因此,每19年相差206.625日,约等于7个朔望月.这样每19年就有7个闰月年.以下是1640年至1694年间所有的闰月年:
日,回归年的总长度为365.2422日,两者相差10.875日.因此,每19年相差206.625日,约等于7个朔望月.这样每19年就有7个闰月年.以下是1640年至1694年间所有的闰月年:
1640 | 1642 | 1645 | 1648 | 1651 | 1653 | 1656 |
1659 | 1661 | 1664 | 1667 | 1670 | 1672 | 1675 |
1678 | 1680 | 1 683 | 1686 | 1689 | 1691 | 1694 |
则从2020年至2049年,这30年间闰月年的个数为( )
A.10B.11C.12D.13
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间![]() 岁之间,对区间
岁之间,对区间![]() 岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:

组数 | 分组 | 人数 |
第一组 |
| 2 |
第二组 |
| a |
第三组 |
| 5 |
第四组 |
| 4 |
第五组 |
| 3 |
第六组 |
| 2 |
(1)求a的值并画出频率分布直方图;
(2)从被调查的20人且年龄在![]() 岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间
岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间![]() 岁年龄段的人数为X,求随机变量X的分布列及数学期望.
岁年龄段的人数为X,求随机变量X的分布列及数学期望.
【题目】疫情过后,某商场开业一周累计生成2万张购物单,从中随机抽出100张,对每单消费金额进行统计得到下表:
消费金额(单位:元) |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 | ? | ? |
由于工作人员失误,后两栏数据已无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等(用频率估计概率),完成下列问题:
(1)估计该商场开业一周累计生成的购物单中,单笔消费额超过800元的购物单张数;
(2)为鼓励顾客消费,拉动内需,该商场打算在今年国庆期间进行促销活动,凡单笔消费超过600元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值![]() 元、
元、![]() 元、
元、![]() 元的奖品.已知中奖率为100%,且一等奖、二等奖、三等奖的中奖率依次构成等差数列,其中一等奖的中奖率为
元的奖品.已知中奖率为100%,且一等奖、二等奖、三等奖的中奖率依次构成等差数列,其中一等奖的中奖率为![]() .若今年国庆期间该商场的购物单数量预计比疫情后开业一周的购物单数量增长5%,试预测商场今年国庆期间采办奖品的开销.
.若今年国庆期间该商场的购物单数量预计比疫情后开业一周的购物单数量增长5%,试预测商场今年国庆期间采办奖品的开销.
