题目内容
【题目】已知椭圆![]() :
:![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,上顶点为点
,上顶点为点![]() ,若
,若![]() 是面积为
是面积为![]() 的等边三角形.
的等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,且
上的两点,且![]() ,求使
,求使![]() 的面积最大时直线
的面积最大时直线![]() 的方程(
的方程(![]() 为坐标原点).
为坐标原点).
【答案】解(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)由![]() 是面积为
是面积为![]() 的等边三角形,结合性质
的等边三角形,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() ,即可得结果;(2)先证明直线
,即可得结果;(2)先证明直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立消去
,与椭圆方程联立消去![]() ,利用弦长公式可得
,利用弦长公式可得 ![]()
![]() ,化简得
,化简得![]() .原点
.原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() 的面积
的面积![]() ,当
,当![]() 最大时,
最大时,![]() 的面积最大.由
的面积最大.由![]() ,利用二次函数的性质可得结果.
,利用二次函数的性质可得结果.
(1)由![]() 是面积为
是面积为![]() 的等边三角形,得
的等边三角形,得![]() ,
,
所以![]() ,
,![]() ,从而
,从而![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由(1)知,当![]() 轴时,
轴时,![]() ,则
,则![]() 为椭圆
为椭圆![]() 的短轴,故有
的短轴,故有![]() ,
,![]() ,
,![]() 三点共线,不合题意.
三点共线,不合题意.
所以直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,点
,点![]() ,联立方程组
,联立方程组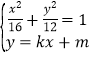 消去
消去![]() ,得
,得![]() ,
,
所以有![]() ,
,![]() ,
,
则![]()
![]() ,
,
即![]() ,化简得
,化简得![]() .
.
因为![]() ,所以有
,所以有![]() 且
且![]() .
.
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() 的面积
的面积![]() ,
,
所以当![]() 最大时,
最大时,![]() 的面积最大.
的面积最大.
因为![]() ,而
,而![]() ,
,
所以当![]() 时,
时,![]() 取最大值为3,
取最大值为3,![]() 面积的最大值
面积的最大值![]() .
.
把![]() 代入
代入![]() ,得
,得![]() ,所以有
,所以有![]() ,
,
即直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】上海市旅游节刚落下帷幕,在旅游节期间,甲、乙、丙三位市民顾客分别获得一些景区门票的折扣消费券,数量如表1,已知这些景区原价和折扣价如表2(单位:元).
表1:
数量 | 景区1 | 景区2 | 景区3 |
甲 | 0 | 2 | 2 |
乙 | 3 | 0 | 1 |
丙 | 4 | 1 | 0 |
表2:
门票 | 景区1 | 景区2 | 景区3 |
原价 | 60 | 90 | 120 |
折扣后价 | 40 | 60 | 80 |
(1)按照上述表格的行列次序分别写出这三位市民获得的折扣消费券数量矩阵A和三个景区的门票折扣后价格矩阵B;
(2)利用你所学的矩阵知识,计算三位市民各获得多少元折扣?