题目内容
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间![]() 岁之间,对区间
岁之间,对区间![]() 岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:

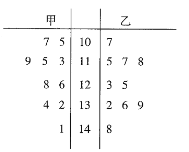
组数 | 分组 | 人数 |
第一组 |
| 2 |
第二组 |
| a |
第三组 |
| 5 |
第四组 |
| 4 |
第五组 |
| 3 |
第六组 |
| 2 |
(1)求a的值并画出频率分布直方图;
(2)从被调查的20人且年龄在![]() 岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间
岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间![]() 岁年龄段的人数为X,求随机变量X的分布列及数学期望.
岁年龄段的人数为X,求随机变量X的分布列及数学期望.
【答案】(1)4,直方图见解析;(2)分布列见解析,2.
【解析】
(1)根据调查总人数可得![]() 的值,计算每组的频率除以组距,即可画出频率分布直方图;
的值,计算每组的频率除以组距,即可画出频率分布直方图;
(2)易知X所有可能取值是1,2,3,利用古典概型可得随机变量取值的概率,即可得到分布列和期望.
(1)![]() ,
,
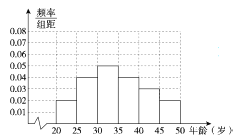
直方图中小矩形的高度依次为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其频率分布直方图如图.
(2)因为区间![]() 岁年龄段的“投资者”有2名,区间
岁年龄段的“投资者”有2名,区间![]() 岁年龄段“投资者”有4名,
岁年龄段“投资者”有4名,
则易知X所有可能取值是1,2,3.
则![]() ;
;![]() ;
;![]() .
.
故随机变量X的分布为
| 1 | 2 | 3 |
|
|
|
|
故随机变量X的数学期望为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:
40岁以下 | 40岁以上 | 合计 | |
很兴趣 | 30 | 15 | 45 |
无兴趣 | 20 | 35 | 55 |
合计 | 50 | 50 | 100 |
(1)根据列联表,能否有![]() 的把握认为对手机游戏的兴趣程度与年龄有关?
的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从![]() 岁以下的被调查者中用分层抽样的方式抽取了
岁以下的被调查者中用分层抽样的方式抽取了![]() 名,现从这
名,现从这![]() 名被调查者中随机选取
名被调查者中随机选取![]() 名,求这
名,求这![]() 名被调查者中恰有
名被调查者中恰有![]() 名对手机游戏无兴趣的概率.
名对手机游戏无兴趣的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.84 | 6.635 | 10.828 |
(注:参考公式: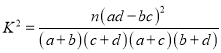 ,其中
,其中![]() )
)
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: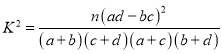 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |