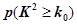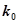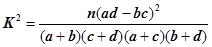题目内容
在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为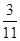 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | | |
| 乙班 | |  | |
| 合计 | | |  |
(2)根据列联表的数据,能否有
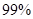 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的
 名学生从
名学生从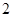 到
到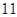 进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到
进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到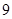 号或
号或 号的概率.
号的概率.
(1)详见解析;(2)按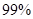 的可靠性要求,能认为“成绩与班级有关系”;
的可靠性要求,能认为“成绩与班级有关系”;
(3)抽到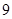 或
或 号的概率为
号的概率为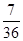 .
.
解析试题分析:(1)先根据题中条件确定乙班优秀的人数,然后根据甲乙两班的总人数将表中其它的数据补充上;(2)先提出假设“成绩与班级无关”,根据表中数据求出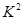 的值,然后利用临界值表确定犯错误的概率,进而确定是否有
的值,然后利用临界值表确定犯错误的概率,进而确定是否有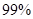 的把握认为成绩与班级有关系;(3)先把事件空间中的基本事件全部列出,并计算基本事件的总数,然后将问题中涉及的事件所包含的基本事件找出来,利用古典概型的概率公式计算所求事件的概率.
的把握认为成绩与班级有关系;(3)先把事件空间中的基本事件全部列出,并计算基本事件的总数,然后将问题中涉及的事件所包含的基本事件找出来,利用古典概型的概率公式计算所求事件的概率.
试题解析:(1)列联表如下表所示:
(2)假设成绩与班级无关,根据列联表中的数据,得到 优秀 非优秀 合计 甲班 
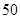
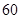
乙班 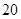

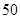
合计 
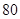

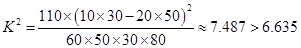 ,
,
因此按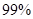 的可靠性要求,能认为“成绩与班级有关系”;
的可靠性要求,能认为“成绩与班级有关系”;
(3)先后两次抛掷一枚均匀的骰子,出现的点数为 ,所有的基本事件有:
,所有的基本事件有: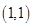 、
、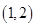 、
、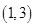 、
、 、
、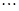 、
、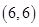 ,共
,共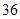 个,
个,
设“抽到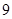 或
或 号”为事件
号”为事件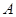 ,
,
事件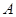 包含的基本事件有:
包含的基本事件有: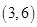 、
、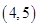 、
、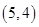 、
、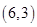 、
、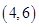 、
、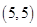 、
、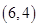 ,共
,共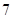 个,
个,
所以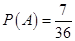 ,即抽到
,即抽到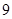 或
或 号的概率为
号的概率为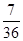 .
.
考点:1.独立性检验;2.古典概型

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
某小组共有 、
、 、
、 、
、 、
、 五位同学,他们的身高(单位:米)以及体重指
五位同学,他们的身高(单位:米)以及体重指
标(单位:千克/米2)如下表所示:
| |  |  |  |  |  |
| 身高 |  |  |  |  |  |
| 体重指标 |  |  |  |  |  |
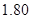 的同学中任选
的同学中任选 人,求选到的
人,求选到的 人身高都在
人身高都在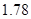 以下的概率;
以下的概率;(2)从该小组同学中任选
 人,求选到的
人,求选到的 人的身高都在
人的身高都在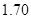 以上且体重指标都在
以上且体重指标都在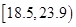 中的概率.
中的概率.  为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
 名男生,
名男生, 名男生,
名男生, 人,请他们在班会上和全班同学分享学习心得.
人,请他们在班会上和全班同学分享学习心得. 名学生作为样本,得到这
名学生作为样本,得到这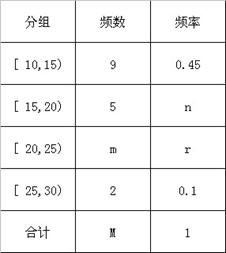
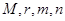 的值;
的值; 次的学生中任选
次的学生中任选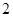 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间 内的概率.
内的概率. .
.