题目内容
设有关于x的一元二次方程 .
.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
⑴ ;⑵
;⑵ .
.
解析试题分析:⑴先列举出满足条件“ 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数”的所有的基本事件,再在基本事件中找到满足条件“
三个数中任取的一个数”的所有的基本事件,再在基本事件中找到满足条件“ ”的基本事件
”的基本事件 的个数,用基本事件
的个数,用基本事件 的个数除以总的事件的个数,所得的比值即是所求;⑵根据
的个数除以总的事件的个数,所得的比值即是所求;⑵根据 的取值画出满足条件“
的取值画出满足条件“ 是从区间
是从区间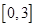 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数”的长方形区域,以及在此条件下满足“
任取的一个数”的长方形区域,以及在此条件下满足“ ”的基本事件的三角形区域,所求的概率即是两个图形的面积比.
”的基本事件的三角形区域,所求的概率即是两个图形的面积比.
试题解析:设事件 为“方程
为“方程 有实根”.
有实根”.
当 时,方程
时,方程 有实根的充要条件为
有实根的充要条件为 .
.
基本事件共有 个:
个: .
.
其中第一个数表示 的取值,第二个数表示
的取值,第二个数表示 的取值.
的取值.
事件 中包含9个基本事件, 4分
中包含9个基本事件, 4分
事件 发生的概率为
发生的概率为 . 6分
. 6分
如图所示:
试验的全部结果所构成的区域为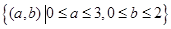 ,对应长方形
,对应长方形 ,8分
,8分
构成事件 的区域为
的区域为 ,对应图中的阴影部分, 10分
,对应图中的阴影部分, 10分
所以所求的概率为 . 12分
. 12分
考点:1.离散型随机变量及其应用;2.连续性随机变量及其应用;3.古典概型;4.几何概型

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为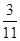 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | | |
| 乙班 | |  | |
| 合计 | | |  |
(2)根据列联表的数据,能否有
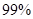 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的
 名学生从
名学生从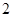 到
到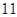 进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到
进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到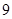 号或
号或 号的概率.
号的概率.  ,求
,求 .
. ,家长所得点数记为
,家长所得点数记为 ;
; ,家长的计算器产生的随机实数记为
,家长的计算器产生的随机实数记为 .
. ,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率; ,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
 、
、 、
、 三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加
三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加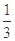 ,丙、丁两人各自通过测试的概率均为
,丙、丁两人各自通过测试的概率均为 .戊参加
.戊参加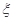 ,求
,求 只,其中有
只,其中有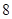 只合格品,
只合格品, 只次品。
只次品。 次,每次取一只灯泡,求
次,每次取一只灯泡,求 的分布列和数学期望.
的分布列和数学期望. .
. 个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得
个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得 分,选对得
分,选对得 分.在这次考试的选择题部分,某考生比较熟悉其中的
分.在这次考试的选择题部分,某考生比较熟悉其中的 个题,该考生做对了这
个题,该考生做对了这 个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题:
个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题: 分的概率;
分的概率; ,求
,求