题目内容
已知函数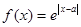 (
(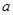 为常数),若
为常数),若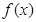 在区间
在区间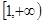 上是单调增函数,则
上是单调增函数,则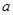 的取值范围是 。
的取值范围是 。
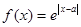 (
(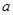 为常数),若
为常数),若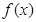 在区间
在区间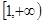 上是单调增函数,则
上是单调增函数,则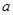 的取值范围是 。
的取值范围是 。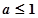 。
。 试题分析:因为
 在R上是单调增函数,
在R上是单调增函数, 在
在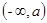 上单调减函数,在
上单调减函数,在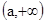 上单调增函数,所以
上单调增函数,所以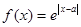 在
在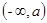 上单调减函数,在
上单调减函数,在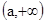 上单调增函数,因此要使
上单调增函数,因此要使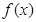 在区间
在区间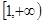 上是单调增函数,需满足
上是单调增函数,需满足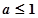 。
。点评:判断复合函数的单调性,只需要满足四个字:同增异减,但一定要注意先求函数的定义域。

练习册系列答案
相关题目
 ,在使
,在使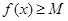 成立的所有常数M中,我们把M的最大值称为函数
成立的所有常数M中,我们把M的最大值称为函数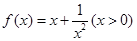 上的“下确界”为 .
上的“下确界”为 .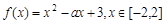 。
。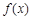 在
在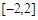 上的最小值是
上的最小值是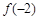 ,试解不等式
,试解不等式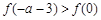 ;
;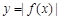 在
在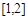 上单调递增,试求实数
上单调递增,试求实数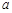 的取值范围。
的取值范围。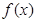 在区间[2,6]上是增函数,且最小值为4,则
在区间[2,6]上是增函数,且最小值为4,则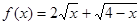 ,则函数
,则函数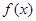 的值域为 ( )
的值域为 ( )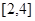


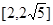
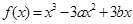
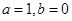 ,求
,求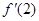 的值;
的值;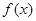 的图像与直线
的图像与直线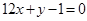 相切于点
相切于点 ,求
,求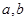 的值;
的值;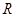 的函数
的函数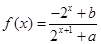 是奇函数。
是奇函数。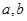 的值;
的值;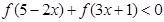
 上的函数
上的函数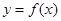 满足下列条件:①对任意的
满足下列条件:①对任意的 都有
都有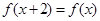 ;②若
;②若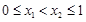 ,都有
,都有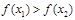 ;③
;③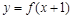 是偶函数,则下列不等式中正确的是()
是偶函数,则下列不等式中正确的是()
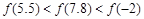
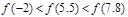

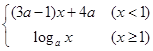 在区间
在区间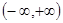 内是减函数,则
内是减函数,则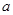 的取值范围是_______.
的取值范围是_______.