Question

【题目】已知函数.

（1）令，若在区间上不单调，求的取值范围；

（2）当时，函数的图象与轴交于两点，，且，又是的导函数.若正常数，满足条件，.试比较与0的关系，并给出理由

Answer 1

【答案】（1）（2）见解析.

【解析】

（1）先求得，因为g（x）在区间（0，3）上不单调，所以g'（x）＝0在（0，3）上有实数解，且无重根．由g'（x）＝0，求得，由此可得a的范围．（2）由题意可得，f（x）﹣mx＝0有两个实根x1，x2，化简可得．可得h′（α+β），由条件知（2α﹣1）（）≤0，利用分析法结合构造函数证明h′（α+β）

（1）因为，所以，

因为在区间上不单调，所以在上有实数解，且无重根，

由，有，，令t=x+1>4

则y=2(t+在t>4单调递增，故

（2）∵，又有两个实根，，

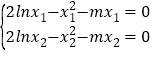∴，两式相减，得，

∴，

于是

.

∵，∴，∴.

要证：，只需证：

只需证：.（*）

令，∴（*）化为，只需证

∵在上单调递增，，∴，即.

∴.