题目内容
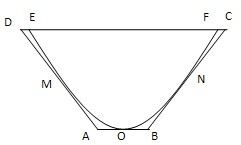
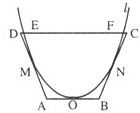
如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米
(1)建立适当的直角坐标系,求抛物线方程.
(2)现将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少?
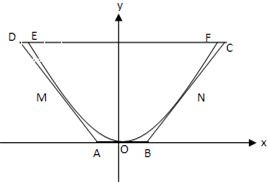
(1)建立适当的直角坐标系,求抛物线方程.
(2)现将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少?

(1)如图以O为原点,AB所在的直线为X轴,建立平面直角坐标系,
则F(2,3),设抛物线的方程是x2=2py(p>0)
因为点F在抛物线上,所以4=2p×3,p=
所以抛物线的方程是x2=
y(5分)
(2)等腰梯形ABCD中,AB∥CD,线段AB的中点O是抛物线的顶点,AD,AB,BC分别与抛物线切于点M,O,N
y'=
x,设N(x0,y0),x0>0,,
则抛物线在N处的切线方程是y-y0=
x0(x-x0),所以B(
x0,0)C(
,3),(10分)
梯形ABCD的面积是S=
(x0+
)×3=
(2x0+
)=3(x0+
)≥6
,等号当且仅当x0=
时成立,
答:梯形ABCD的下底AB=
米时,所挖的土最少(12分)
则F(2,3),设抛物线的方程是x2=2py(p>0)
因为点F在抛物线上,所以4=2p×3,p=
| 2 |
| 3 |
所以抛物线的方程是x2=
| 4 |
| 3 |
(2)等腰梯形ABCD中,AB∥CD,线段AB的中点O是抛物线的顶点,AD,AB,BC分别与抛物线切于点M,O,N
y'=
| 3 |
| 2 |
则抛物线在N处的切线方程是y-y0=
| 3 |
| 2 |
| 1 |
| 2 |
| 4+x02 |
| 2x0 |
梯形ABCD的面积是S=
| 1 |
| 2 |
| 4+x02 |
| 2x0 |
| 3 |
| 2 |
| 4 |
| x0 |
| 2 |
| x0 |
| 2 |
| 2 |
答:梯形ABCD的下底AB=
| 2 |


练习册系列答案
相关题目
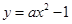 ,直线
,直线 的方程为
的方程为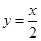 ,点
,点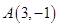 关于直线
关于直线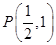 ,点
,点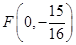 是抛物线的焦点,
是抛物线的焦点,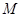 是抛物线上的动点,求
是抛物线上的动点,求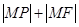 的最小值及此时点
的最小值及此时点 、
、 是抛物线上的动点,点
是抛物线上的动点,点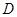 是抛物线与
是抛物线与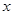 轴正半轴交点,
轴正半轴交点, 是以
是以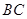 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. 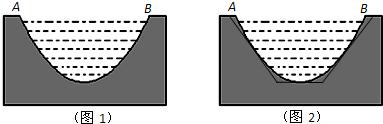
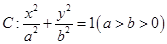 的左右焦点为
的左右焦点为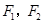 ,作
,作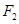 作
作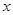 轴的垂线与
轴的垂线与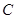 交于
交于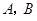 两点,
两点,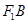 与
与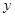 轴交于点
轴交于点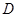 ,若
,若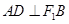 ,则椭圆
,则椭圆