题目内容
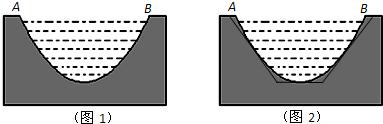
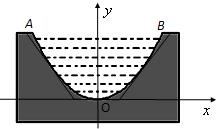
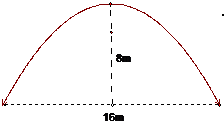
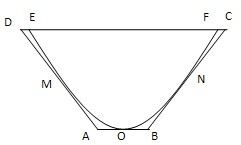
一个截面为抛物线形的旧河道(如图1),河口宽AB=4米,河深2米,现要将其截面改造为等腰梯形(如图2),要求河道深度不变,而且施工时只能挖土,不准向河道填土.
(1)建立恰当的直角坐标系并求出抛物线弧AB的标准方程;
(2)试求当截面梯形的下底(较长的底边)长为多少米时,才能使挖出的土最少?
(1)建立恰当的直角坐标系并求出抛物线弧AB的标准方程;
(2)试求当截面梯形的下底(较长的底边)长为多少米时,才能使挖出的土最少?

(1)如图:以抛物线的顶点为原点,AB中垂线为y轴建立直角坐标系
则A(-2,2),B(2,2)
设抛物线的方程为x2=2Py(P>0),
将点B(2,2)代入得P=1
所以抛物线弧AB方程为x2=2y(-2≤x≤2)
(2)设等腰梯形的腰与抛物线相切于P(t,
t2),(不妨t>0)
则过P(t,
t2)的切线l的斜率为y′|x=t=t
所以切线l的方程为:y-
=t(x-t),即y=tx-
令y=0,得x=
,
令y=2,得x=
+
,
所以梯形面积S=
[2•(
+
)+2•
]•2=2(t+
)≥4
当仅当t=
,即t=
时,“=”成立
此时下底边长为2(
+
)=3
答:当梯形的下底边长等于3
米时,挖出的土最少.
则A(-2,2),B(2,2)
设抛物线的方程为x2=2Py(P>0),
将点B(2,2)代入得P=1
所以抛物线弧AB方程为x2=2y(-2≤x≤2)
(2)设等腰梯形的腰与抛物线相切于P(t,
| 1 |
| 2 |
则过P(t,
| 1 |
| 2 |
所以切线l的方程为:y-
| t2 |
| 2 |
| t2 |
| 2 |
令y=0,得x=
| t |
| 2 |
令y=2,得x=
| t |
| 2 |
| 2 |
| t |
所以梯形面积S=
| 1 |
| 2 |
| t |
| 2 |
| 2 |
| t |
| t |
| 2 |
| 2 |
| t |
| 2 |
当仅当t=
| 2 |
| t |
| 2 |
此时下底边长为2(
| ||
| 2 |
| 2 | ||
|
| 2 |
答:当梯形的下底边长等于3
| 2 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
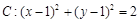 经过椭圆
经过椭圆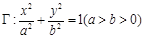 的右焦点
的右焦点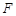 和上顶点
和上顶点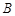 .
. 的方程;
的方程;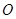 的射线
的射线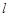 与椭圆
与椭圆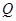 ,与圆
,与圆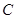 的交点为
的交点为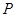 ,
,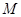 为
为 的中点,求
的中点,求 的最大值.
的最大值.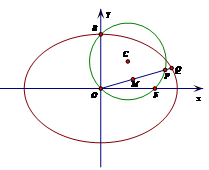
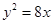 的焦点为F,准线为
的焦点为F,准线为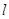 ,P是
,P是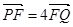 ,则
,则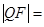 ( )
( )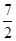
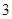
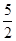
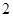
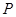 是双曲线
是双曲线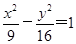 的右支上一点,
的右支上一点,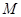 、
、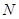 分别是圆
分别是圆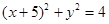 和
和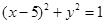 上的点,则
上的点,则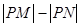 的最大值等于 .
的最大值等于 .