题目内容
已知抛物线C:y2=2px,点P(-1,0)是其准线与x轴的焦点,过P的直线l与抛物线C交于A、B两点.
(1)当线段AB的中点在直线x=7上时,求直线l的方程;
(2)设F为抛物线C的焦点,当A为线段PB中点时,求△FAB的面积.
(1)当线段AB的中点在直线x=7上时,求直线l的方程;
(2)设F为抛物线C的焦点,当A为线段PB中点时,求△FAB的面积.
(1)因为抛物线的准线为x=-1,所以p=2,抛物线方程为y2=4x(2分)
设A(x1,y1),B(x2,y2),直线l的方程为y=k(x+1),(依题意k存在,且k≠0)与抛物线方程联立,消去y得k2x2+(2k2-4)x+k2=0…(*)x1+x2=
,x1x2=(14分)
所以AB中点的横坐标为
,即
=7所以k2=
(6分)
(此时(*)式判别式大于零)
所以直线l的方程为y=±
(x+1)(7分)
(2)因为A为线段PB中点,所以
=x1,
=y1(8分)
由A、B为抛物线上点,得(
)2=4×
,y22=4x2(10分)
解得x2=2,y2=±2
(11分)
当y2=2
时,y1=
;当y2=-2
时,y1=-
(12分)
所以△FAB的面积S△FAB=S△PFB-S△PFA=
|PF|•|y2-y|=
(14分)

设A(x1,y1),B(x2,y2),直线l的方程为y=k(x+1),(依题意k存在,且k≠0)与抛物线方程联立,消去y得k2x2+(2k2-4)x+k2=0…(*)x1+x2=
| 4-2k2 |
| k2 |
所以AB中点的横坐标为
| 2-k2 |
| k |
| 2-k2 |
| k2 |
| 1 |
| 4 |
(此时(*)式判别式大于零)
所以直线l的方程为y=±
| 1 |
| 2 |
(2)因为A为线段PB中点,所以
| x2-1 |
| 2 |
| y2 |
| 2 |
由A、B为抛物线上点,得(
| y2 |
| 2 |
| x2-1 |
| 2 |
解得x2=2,y2=±2
| 2 |
当y2=2
| 2 |
| 2 |
| 2 |
| 2 |
所以△FAB的面积S△FAB=S△PFB-S△PFA=
| 1 |
| 2 |
| 2 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
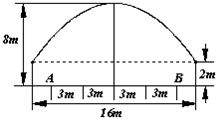
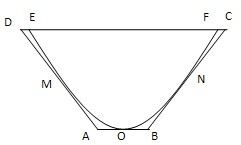
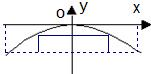
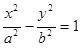
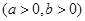 的一个焦点与抛物线
的一个焦点与抛物线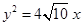 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于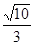 ,则该双曲线的方程为( )
,则该双曲线的方程为( )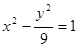
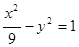
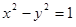
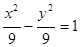
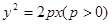 的焦点为
的焦点为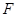 ,已知
,已知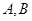 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足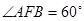 ,过弦
,过弦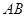 的中点
的中点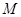 作抛物线准线的垂线
作抛物线准线的垂线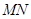 ,垂足为
,垂足为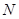 ,则
,则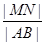 的最大值为 .
的最大值为 .