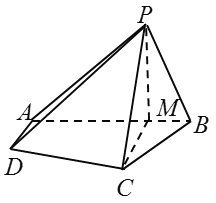
[题目]设点.是平面上左.右两个不同的定点. .动点满足:．(1)求证:动点的轨迹为椭圆,(2)抛物线满足:①顶点在椭圆的中心,②焦点与椭圆的右焦点重合．设抛物线与椭圆的一个交点为．问:是否存在正实数.使得的边长为连续自然数．若存在.求出的值,若不存在.说明理由．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】设点、是平面上左、右两个不同的定点，，动点满足：

．

（1）求证：动点的轨迹为椭圆；

（2）抛物线满足：①顶点在椭圆的中心；②焦点与椭圆的右焦点重合．

设抛物线与椭圆的一个交点为．问：是否存在正实数，使得的边长为连续自然数．若存在，求出的值；若不存在，说明理由．

【答案】（1）见解析；（2）存在实数，使得的边长为连续自然数。

【解析】试题分析: （1）根据题意，分两种情况讨论：①点P、F1、F2构成三角形，②点P、F1、F2不构成三角形，每种情况下分析可得|PF1|+|PF2|=4m，由椭圆的定义分析可得答案；

（2）根据题意，由（1）可得，动点P的轨迹方程，分析可得抛物线的焦点坐标，假设存在满足条件的实数m，结合椭圆与抛物线的性质分析可得m的值，即可得答案．

试题解析

（1）若点构成三角形则

，

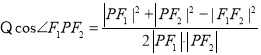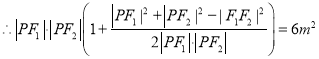
整理得，即．

若点不构成三角形，也满足．

所以动点的轨迹为椭圆

（2）动点的轨迹方程为

抛物线的焦点坐标为与椭圆的右焦点重合．

假设存在实数，使得的边长为连续自然数．

因为，

不妨设|，

由抛物线的定义可知，解得，

设点的坐标为，

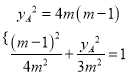
整理得，解得或

所以存在实数，使得的边长为连续自然数

练习册系列答案

相关题目

【题目】已知函数，．

（Ⅰ）求曲线在处的切线方程．

（Ⅱ）求的单调区间．

（Ⅲ）设，其中，证明：函数仅有一个零点．

【题目】在四棱锥中，，，点M是线段AB上的一点，且．

（1）证明：平面平面ABCD；

（2）求直线CM与平面PCD所成角的正弦值．

【题目】已知，为实数，函数，函数．

(1) 当时，令，若恒成立，求实数的取值范围；

(2) 当时，令，是否存在实数，使得对于函数定义域中的任意实数，均存在实数，有成立？若存在，求出实数的取值集合；若不存在，请说明理由．

【题目】已知数列满足，，其中.

（1）设，求证：数列是等差数列，并求出的通项公式；

（2）设，数列的前项和为，是否存在正整数，使得对于恒成立，若存在，求出的最小值，若不存在，请说明理由.

【题目】设函数，．

（Ⅰ）若，求的极小值；

（Ⅱ）在（Ⅰ）的条件下，是否存在实常数和，使得和？若存在，求出和的值．若不存在，说明理由；

（Ⅲ）设有两个零点，且成等差数列，试探究值的符号．

【题目】要分析学生初中升学考试的数学成绩对高一年级数学学习有什么影响，在高一年级学生中随机抽取10名学生，分析他们入学的数学成绩(x)和高一年级期末数学考试成绩(y)(如下表)：

(1)画出散点图；

(2)判断入学成绩(x)与高一期末考试成绩(y)是否有线性相关关系；

(3)如果x与y具有线性相关关系，求出回归直线方程；

编号	1	2	3	4	5	6	7	8	9	10
x	63	67	45	88	81	71	52	99	58	76
y	65	78	52	85	92	89	73	98	56	75

【题目】某花店每天以每枝元的价格从农场购进若干枝玫瑰花，然后以每枝元的价格出售.如果当天卖不完，剩下的玫瑰花做垃圾处理.

（1）若花店一天购进枝玫瑰花，求当天的利润（单位：元）关于当天需求量（单位：枝，）的函数解析式.

（2）花店记录了天玫瑰花的日需求量（单位：枝），整理得下表：

日需求量
频数

假设花店在这天内每天购进枝玫瑰花，求这天的日利润（单位：元）的平均数.

【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之，问各出几何？此问题的译文是:今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还，他们各应偿还多少？已知牛、马、羊的主人各应偿还升，升，升，1斗为10升，则下列判断正确的是( )