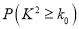题目内容
【题目】已知![]() 是由正整数组成的无穷数列,该数列前
是由正整数组成的无穷数列,该数列前![]() 项的最大值记为
项的最大值记为![]() ,第
,第![]() 项之后各项
项之后各项![]() ,
, ![]() ,
, ![]() 的最小值记为
的最小值记为![]() ,
, ![]() .
.
(I)若![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,是一个周期为
,是一个周期为![]() 的数列(即对任意
的数列(即对任意![]() ,
, ![]() ),写出
),写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(II)设![]() 是正整数,证明:
是正整数,证明: ![]() 的充分必要条件为
的充分必要条件为![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(III)证明:若![]() ,
, ![]() ,则
,则![]() 的项只能是
的项只能是![]() 或者
或者![]() ,且有无穷多项为
,且有无穷多项为![]() .
.
【答案】(I)![]() ,
, ![]() ;(II)见解析;(III)见解析.
;(II)见解析;(III)见解析.
【解析】试题分析:(I)根据已知给出的![]() 的定义,直接求出
的定义,直接求出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(II)分别证明充分性和必要性。充分性:由条件![]() 是公比为
是公比为![]() 的等比数列且
的等比数列且![]() 为正整数,推导结论
为正整数,推导结论![]() ;必要性:由结论推导条件。
;必要性:由结论推导条件。
(III)本问采用反证法,假设![]() 中存在大于
中存在大于![]() 的项,推导出矛盾。即可得到假设不成立,故
的项,推导出矛盾。即可得到假设不成立,故![]() 中没有大于2的项,又由于
中没有大于2的项,又由于![]() 是由正整数组成的无穷数列,故
是由正整数组成的无穷数列,故![]() 中只可能是1和2.然后再进一步证明数列中存在无穷多个1.
中只可能是1和2.然后再进一步证明数列中存在无穷多个1.
试题解析:(I)由题知,在![]() 中,
中,
![]() ,
,
![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
(II)证明:
充分性:∵![]() 是公比为
是公比为![]() 的等比数列且
的等比数列且![]() 为正整数,
为正整数,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,(
,( ![]() ,
, ![]() ,
, ![]() ).
).
必要性:∵![]() ,(
,( ![]() ,
, ![]() ,
, ![]() ),
),
∴![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() 为公比为
为公比为![]() 的等比数列.
的等比数列.
(III)∵![]() ,
, ![]() ,
,
∴![]() ,
,
![]() ,
,
∴对任意![]() ,
, ![]() ,
,
假设![]() 中存在大于
中存在大于![]() 的项,
的项,
设![]() 为满足
为满足![]() 的最小正整数,
的最小正整数,
则![]() ,对任意
,对任意![]() ,
, ![]() ,
,
又∵![]() ,∴
,∴![]() 且
且![]() ,
,
∴![]() ,
,
![]() ,
, ![]() ,
,
故![]() 与
与![]() 矛盾,
矛盾,
∴对于任意![]() ,有
,有![]() ,
,
即非负整数列![]() 各项只能为
各项只能为![]() 或
或![]() .
.

【题目】近年来许多地市空气污染较为严重,现随机抽取某市一年(365天)内100天的![]() 空气质量指数(
空气质量指数(![]() )的监测数据,统计结果如表:
)的监测数据,统计结果如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 4 | 13 | 18 | 30 | 20 | 15 |
记某企业每天由空气污染造成的经济损失为![]() (单位:元),
(单位:元),![]() 指数为
指数为.当
![]() 在区间
在区间![]() 内时,对企业没有造成经济损失;当
内时,对企业没有造成经济损失;当![]() 在区间
在区间![]() 内时,对企业造成的经济损失与
内时,对企业造成的经济损失与![]() 成直线模型(当
成直线模型(当![]() 指数为150时,造成的经济损失为1100元,当
指数为150时,造成的经济损失为1100元,当![]() 指数为200时,造成的经济损失为1400元);当
指数为200时,造成的经济损失为1400元);当![]() 指数大于300时,造成的经济损失为2000元.
指数大于300时,造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取1天,该天经济损失![]() 大于1100且不超过1700元的概率;
大于1100且不超过1700元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,这30天中有8天为严重污染,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该市本年度空气严重污染与供暖有关?
的把握认为该市本年度空气严重污染与供暖有关?
非严重污染 | 严重污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 |
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
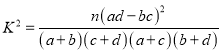 ,其中
,其中![]()