题目内容
函数y=f(x)的图象是两条直线的一部分(如图所示),其定义域为[-1,0)∪(0,1],则不等式f(x)-f(-x)>-1的解集为______.
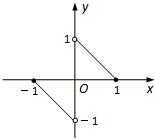

观察函数的图象可知y=f(x)为奇函数,
∴f(x)-f(-x)>-1?2f(x)>-1,
∴f(x)>-
.
∴y=f(x)和y=-
的交点的横坐标为-
,
根据不等式的几何意义观察图象知y=f(x)图象在y=-
上方部分即得到f(x)-f(-x)>-1的解集.
∴f(x)-f(-x)>-1的解集为[-1,-
)∪(0,1].
故答案为:[-1,-
)∪(0,1].
∴f(x)-f(-x)>-1?2f(x)>-1,
∴f(x)>-
| 1 |
| 2 |
∴y=f(x)和y=-
| 1 |
| 2 |
| 1 |
| 2 |
根据不等式的几何意义观察图象知y=f(x)图象在y=-
| 1 |
| 2 |
∴f(x)-f(-x)>-1的解集为[-1,-
| 1 |
| 2 |
故答案为:[-1,-
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
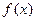 的定义域为R,若存在常数
的定义域为R,若存在常数 ,使
,使 对一切实数
对一切实数 均成立,则称
均成立,则称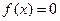 ;②
;②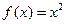 ;③
;③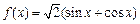 ;④
;④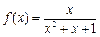 ;⑤
;⑤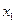 ,
,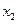 均有
均有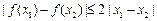 .其中是“倍约束函数”的序号是
.其中是“倍约束函数”的序号是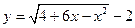
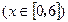 的图像绕坐标原点逆时针方向旋转角
的图像绕坐标原点逆时针方向旋转角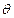
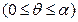 ,得到曲线
,得到曲线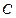 .若对于每一个旋转角
.若对于每一个旋转角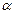 的最大值为__________
的最大值为__________
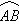 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在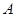 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合,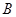 表示具有如下性质的函数
表示具有如下性质的函数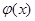 组成的集合:对于函数
组成的集合:对于函数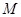 ,使得函数
,使得函数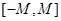 .例如,当
.例如,当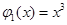 ,
,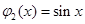 时,
时,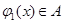 ,
,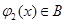 .现有如下命题:
.现有如下命题: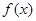 的定义域为
的定义域为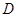 ,则“
,则“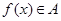 ”的充要条件是“
”的充要条件是“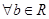 ,
,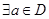 ,
,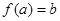 ”;
”;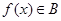 的充要条件是
的充要条件是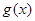 的定义域相同,且
的定义域相同,且 ,则
,则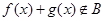 ;
;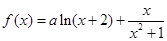 (
(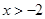 ,
,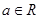 )有最大值,则
)有最大值,则