题目内容
16.设f(x)是定义在R上的函数,且满足f(x+2)=f(x+1)-f(x),如果f(1)=lg$\frac{3}{2}$,f(2)=lg15,则f(2016)=-1.分析 由已知条件推导出f(x)是一个周期为6的函数,所以f(2016)=f(6×336+0)=f(0),利用已知条件求解即可.
解答 解:(1)f(1)=lg$\frac{3}{2}$,f(2)=lg15,
∴f(3)=f(2)-f(1)=lg15-(lg3-lg2)=lg5+lg2=1,
f(4)=f(3)-f(2)=1-lg15,
f(5)=f(4)-f(3)=1-lg15-1=-lg15,
f(6)=f(5)-f(4)=-lg15-(1-lg15)=-1,
f(7)=f(6)-f(5)=-1+lg15=lg$\frac{3}{2}$,
∴f(x)是一个周期为6的函数,
∴f(2016)=f(6×336+1)=f(0),f(2)=f(1)-f(0),
∴f(0)=f(1)-f(2)=lg$\frac{3}{2}$-lg15=lg$\frac{1}{10}$=-1,
故答案为:-1.
点评 本题考查抽象函数的应用,函数值的求法,解题时要认真审题,注意函数的周期性和对数性质的灵活运用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
7.在复平面内复数$z=\frac{ai+1}{1-i}$对应的点在第一象限,则实数a的取值可以为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
1.下列能表示函数图象的是( )
| A. | 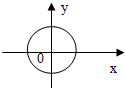 | B. | 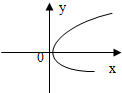 | C. |  | D. | 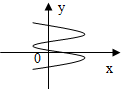 |
5.已知log${\;}_{\frac{1}{2}}$a<log${\;}_{\frac{1}{2}}$b,则下列不等式一定成立的是( )
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | ${({\frac{1}{3}})^a}>{({\frac{1}{3}})^b}$ | C. | ln(a-b)>0 | D. | 3a-b>1 |