题目内容
【题目】设函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)若![]() 使得不等式
使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2) ![]() ;
;
【解析】
(1)求函数的导数,研究函数的单调性即可
(2)利用参数分离法转化为最值问题,构造函数求函数的最值即可
(1)当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)![]() ,使得不等式
,使得不等式![]() 成立.
成立.
即![]() ,使得不等式
,使得不等式![]() 成立.
成立.
等价于![]() ,使得不等式
,使得不等式![]() 成立.
成立.
令![]() ,
,![]() ,则
,则![]() .
.
设![]() ,则
,则![]() ,
,
显然函数![]() 在
在![]() 是增函数.
是增函数.
因为![]() ,
,![]() ,且函数
,且函数![]() 的图象在
的图象在![]() 上连续,
上连续,
所以![]() ,使得
,使得![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数![]() 存在极小值
存在极小值![]() ,也是最小值.
,也是最小值.
所以![]() ,
,
其中![]() ,满足
,满足![]() ,即
,即![]() .
.
所以![]() ,即
,即![]() .
.
所以![]()
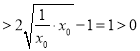 .
.
所以当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 内单调递增.
内单调递增.
所以![]()
![]() .
.
所以有![]() ,
,
即实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目

