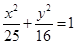题目内容
已知在函数 的图象上,相邻的一个最大值点与一个最小值点恰好在
的图象上,相邻的一个最大值点与一个最小值点恰好在 上,则
上,则 的最小正周期为
的最小正周期为
| A.1 | B.2 | C.3 | D.4 |
D
解析试题分析:∵x2+y2=r2,∴x∈[-r,r].
∵函数f(x)的最小正周期为2r,
∴最大值点为(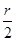 ,
,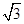 ),相邻的最小值点为(-
),相邻的最小值点为(-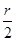 ,-
,-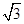 ),
),
代入圆方程,得r=2,∴T=4.
故选D.
考点:本题主要考查三角函数的周期性,圆的对称性.
点评:简单题,关键是理解三角函数两相邻的最大值与最小值正好等于半个周期。

练习册系列答案
相关题目
已知 ,则
,则 的取值范围是( )
的取值范围是( )
A.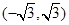 | B.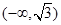 | C.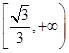 | D. |
圆x2+y2+2x-4y=0的圆心坐标和半径分别是( )
| A.(1,-2),5 | B.(1,-2), |
| C.(-1,2),5 | D.(-1,2), |
若关于 的方程组
的方程组 有实数解,则实数
有实数解,则实数 满足( )
满足( )
A. | B. | C. | D. |
圆O的方程为 ,圆M方程为
,圆M方程为 ,P为圆M上任一点,过P作圆O的切线PA,若PA与圆M的另一个交点为Q,当弦PQ的长度最大时,切线PA的斜率是( )
,P为圆M上任一点,过P作圆O的切线PA,若PA与圆M的另一个交点为Q,当弦PQ的长度最大时,切线PA的斜率是( )
| A.7或1 | B. 或1 或1 | C. 或-1 或-1 | D.7或-1 |
若圆 上有且只有两个点到直线
上有且只有两个点到直线 的距离为1,则半径
的距离为1,则半径 的取值范围是( )
的取值范围是( )
A.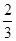 | B. | C. | D.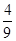 |
若圆 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴相切,则该圆的标准方程是( )
轴相切,则该圆的标准方程是( )
A. | B. |
C. | D. |
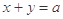 与圆
与圆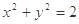 交于A、B两点,O是原点,若
交于A、B两点,O是原点,若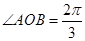 ,则
,则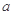 的值为( )
的值为( )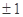 B.
B.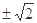 C.
C.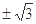 D.
D.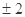
 和点B(3,0),P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。
和点B(3,0),P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。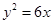 .
.