题目内容
若圆 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴相切,则该圆的标准方程是( )
轴相切,则该圆的标准方程是( )
A. | B. |
C. | D. |
A
解析试题分析:设圆心坐标为(a,b)(a>0,b>0),
由圆与直线4x-3y=0相切,可得圆心到直线的距离d= ,化简得:|4a-3b|=5①,
,化简得:|4a-3b|=5①,
又圆与x轴相切,可得|b|=r=1,解得b=1或b=-1(舍去),
把b=1代入①得:4a-3=5或4a-3=-5,解得a=2或a=-
(舍去),∴圆心坐标为(2,1),
则圆的标准方程为:(x-2)2+(y-1)2=1.
故选A
考点:圆的方程的求解
点评:此题考查了直线与圆的位置关系,以及圆的标准方程,若直线与圆相切时,圆心到直线的距离d等于圆的半径r,要求学生灵活运用点到直线的距离公式,以及会根据圆心坐标和半径写出圆的标准方程。

练习册系列答案
相关题目
已知在函数 的图象上,相邻的一个最大值点与一个最小值点恰好在
的图象上,相邻的一个最大值点与一个最小值点恰好在 上,则
上,则 的最小正周期为
的最小正周期为
| A.1 | B.2 | C.3 | D.4 |
已知直线 与圆
与圆 相交于
相交于 两点,且
两点,且 则
则 的值是
的值是
A. | B. | C. | D.0 |
圆 上的点到直线
上的点到直线 距离的最大值是( )
距离的最大值是( )
A. | B. | C. | D. |
若圆C的半径为1,圆心在第一象限,且与直线 和
和 轴都相切,则该圆的标准方程是( )
轴都相切,则该圆的标准方程是( )
A. | B.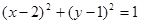 |
C. | D. |
若直线 与圆
与圆 相交于P、Q两点,且∠POQ=120°(其中O为原点),则k的值为( )
相交于P、Q两点,且∠POQ=120°(其中O为原点),则k的值为( )
A. | B. | C. | D. |
过点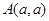 可作圆
可作圆 的两条切线,则实数
的两条切线,则实数 的取值范围为( )
的取值范围为( )
A. 或 或 | B.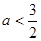 |
C. 或 或 | D. 或 或 |
直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B. | C. | D. |
已知Rt△ABC的两条直角边长分别为a、b,斜边长为c,则直线ax+by+c=0与圆x2+y2=1的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.相切或相交 |